Y=x(x-1)^3 построить график рациональных функций, полное расследование функций

Показать ответ

Ответ:

Moran1

24.08.2021 11:59

1. Найдите значение производной функции в точке x₀:

a) y=(3·x-2)⁷, x₀=3

y'=((3·x-2)⁷)'=7·(3·x-2)⁶·(3·x-2)'=7·(3·x-2)⁶·3=21·(3·x-2)⁶

y'(3)=21·(3·3-2)⁶=21·7⁶=21·117649=2470629

б) y=(4-5·x)⁷, x₀=1

y'=((4-5·x)⁷)'=7·(4-5·x)⁶·(4-5·x)'=7·(4-5·x)⁶·(-5)= -35·(4-5·x)⁶

y'(1)= -35·(4-5·1)⁶= -35·(-1)⁶= -35·1= -35

в) y=(2·x+3)⁵, x₀=2

y'=((2·x+3)⁵)'=5·(2·x+3)⁴·(2·x+3)'=5·(2·x+3)⁴·2=10·(2·x+3)⁴

y'(2)=10·(2·2+3)⁴=10·7⁴=10·2401=24010

г) y=(5-3·x)⁷, x₀=1

y'=((5-3·x)⁷)'=7·(5-3·x)⁶·(5-3·x)'=7·(5-3·x)⁶·(-3)= -21·(5-3·x)⁶

y'(1)= -21·(5-3·1)⁶= -21·2⁶= -21·64= -1344

2. Вычислить скорость изменения функции в точке x₀ (скорость изменения равносильно производная первого порядка):

a) y=(2x+1)⁵, x₀= -1

y'=((2·x+1)⁵)'=5·(2·x+1)⁴·(2·x+1)'=5·(2·x+1)⁴·2=10·(2·x+1)⁴

y'(-1)=10·(2·(-1)+1)⁴=10·(-1)⁴=10·1=10

б)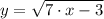 $\displaystyle y=\sqrt{7 \cdot x-3}$ , x₀= 1

$\displaystyle y'=(\sqrt{7 \cdot x-3})' =((7 \cdot x-3)^{\frac{1}{2} })'=\dfrac{1}{2} \cdot (7 \cdot x-3)^{\frac{1}{2}-1} \cdot (7 \cdot x-3)'=\\\\=\dfrac{1}{2} \cdot (7 \cdot x-3)^{-\frac{1}{2}} \cdot 7=\dfrac{7}{2} \cdot (7 \cdot x-3)^{-\frac{1}{2}}$

$\displaystyle y'(1)=\dfrac{7}{2} \cdot (7 \cdot 1-3)^{-\frac{1}{2}}=\dfrac{7}{2} \cdot 4^{-\frac{1}{2}}=\dfrac{7}{2} \cdot 2^{-1}= \dfrac{7}{2} \cdot\frac{1}{2}=\dfrac{7}{4}=1\dfrac{3}{4}$

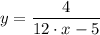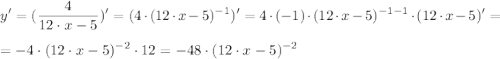
в) $\displaystyle y=\frac{4}{12 \cdot x-5}$ , x₀= 2 $\displaystyle$ $\displaystyle y'=(\frac{4}{12 \cdot x-5})'=(4 \cdot (12 \cdot x-5)^{-1})'=4 \cdot (-1) \cdot (12 \cdot x-5)^{-1-1} \cdot (12 \cdot x-5)'=\\\\=-4 \cdot (12 \cdot x-5)^{-2} \cdot 12=-48 \cdot (12 \cdot x-5)^{-2}$

$\displaystyle y'(2)=-48 \cdot (12 \cdot 2-5)^{-2}= \frac{-48 }{19^{2}}=-\frac{48 }{361}}$

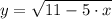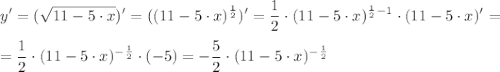
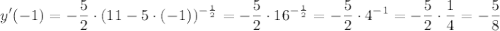
г) $\displaystyle y=\sqrt{11-5 \cdot x}$ , x₀= -1 $\displaystyle y'=(\sqrt{11-5 \cdot x})' =((11-5 \cdot x)^{\frac{1}{2} })'=\dfrac{1}{2} \cdot (11-5 \cdot x)^{\frac{1}{2}-1} \cdot (11-5 \cdot x)'=\\\\=\dfrac{1}{2} \cdot (11-5 \cdot x)^{-\frac{1}{2}} \cdot (-5)=-\dfrac{5}{2} \cdot (11-5 \cdot x)^{-\frac{1}{2}}$ $\displaystyle y'(-1)=-\dfrac{5}{2} \cdot (11-5 \cdot (-1))^{-\frac{1}{2}}=-\dfrac{5}{2} \cdot 16^{-\frac{1}{2}}=-\dfrac{5}{2} \cdot 4^{-1}= -\dfrac{5}{2} \cdot \frac{1}{4}=-\dfrac{5}{8}$

3. Найдите производные функций:

a) y=(x-1)·(x²+x+1) = x³-1

=1·(x²+x+1)+(x-1)·(2·x+1)= x²+x+1+2·x²+x-2·x-1 =3·x²

б)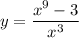 $\displaystyle y=\frac{x^{9}-3}{x^{3}}$

$\displaystyle y'=(\dfrac{x^{9}-3}{x^{3}})'=\dfrac{(x^{9}-3)' \cdot x^{3}-(x^{3})' \cdot (x^{9}-3)}{(x^{3})^{2}}=\\\\=\dfrac{(9 \cdot x^{8}-0) \cdot x^{3}-(3 \cdot x^{2}) \cdot (x^{9}-3)}{x^{6}}=\dfrac{9 \cdot x^{8}\cdot x^{3}-3 \cdot x^{2} \cdot (x^{9}-3)}{x^{6}}=\\\\=\dfrac{9 \cdot x^{11}-3 \cdot x^{11} +9\cdot x^{2}}{x^{6}}=\dfrac{6 \cdot x^{11}+9\cdot x^{2}}{x^{6}}=\dfrac{6 \cdot x^{9}+9}{x^{4}}$

$\displaystyle y'=(\dfrac{x^{9}-3}{x^{3}})'=(x^{6}-\dfrac{3}{x^{3}})'=(x^{6}-3 \cdot x^{-3})'=(x^{6})'-3 \cdot (x^{-3})'=\\\\= 6 \cdot x^{5}-3 \cdot (-3) \cdot x^{-4}=6 \cdot x^{5}+9\cdot x^{-4}=\dfrac{6 \cdot x^{9}+9}{x^{4}}$

0,0(0 оценок)

Ответ:

Машуничка12

01.06.2020 05:33

В задании где-то ошибка. Дело в том, что заданный график функции y=3x²-6x это парабола, ветви которой направлены вверх, вершина параболы находится в точке с координатами (1;-3), поэтому в точке (1;-4) не может быть точка касания.
Если предположить, что точка касания (1;-3), то решение будет следующим:
Уравнение касательной
y=f(x₀)+f'(x₀)(x-x₀)
Так как (1;-3) точка касания, то x₀=1 f(x₀)=-3
Остаётся найти производную и, затем, её значение в точке х₀=1
f'(x)=(3x²-6x)'=6x-6
f'(1)=6*1-6=0
Подставляем все найденные значения в уравнение касательной
y=-3+0*(x-1)=-3
Уравнение касательной - прямая параллельная оси ОХ, проходящая через точку у=-3.

0,0(0 оценок)

Популярные вопросы: Математика