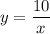Математика: Які 4 значення Х задовольняють нерівність -5/19 Х -4/19

Які 4 значення Х задовольняють нерівність -5/19<Х<-4/19

Показать ответ

Ответ:

500о

25.01.2022 14:19

Телевизоров - 40шт.

Компьютеров - ?, на 24шт. <

Всего - ?шт.

1) 40 - 24 = 16 (шт.) - компьютеров.

2) 40 + 16 = 56 (шт.) - всего.

ответ : 56 штук всего.

Пошаговое объяснение:

Для того что бы узнать сколько всего электроники привезли в магазин, надо посмотреть сколько привезли телевизоров и компьютеров. Сколько привезли компьютеров нам неизвестно, но известно что их привезли на 24 меньше чем телевизоров, а телевизоров у нас 40. Для того чтобы узнать сколько компьютеров надо из 40 вычесть 24. 40 - 24, это будет 16. теперь нам известно сколько телевизоров и компьютеров, а сколько электроники ВСЕГО в магазине нам неизвестно. Чтобы найти сумму надо сложить первое и второе слагаемое. 40 + 16, это будет 56.

Отметьте как лучшее

0,0(0 оценок)

Ответ:

lmarusia

10.01.2020 17:57

Найдите уравнение кривой, проходящей через точку M(2,5) и обладающей свойством, что отрезок любой ее касательной, заключенный между осями координат, делится пополам в точке касания.

По геометрическому смыслу производной

$y'={\rm tg}\alpha=k$

Пусть точка касания имеет координаты (x;y), тогда касательная отсекает на осях отрезки 2х и 2у. Угловой коэффициент касательной равен -y/x. Имеем дифференциальное уравнение: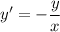 $y'=-\dfrac{y}{x}$ с начальным условием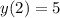 y(2)=5

Данное дифференциальное уравнение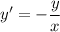 $y'=-\dfrac{y}{x}$ является уравнением с разделяющимися переменными.

$\dfrac{dy}{dx}=-\dfrac{y}{x}~~~\Leftrightarrow~~~\displaystyle \int \dfrac{dy}{y}=-\int \dfrac{dx}{x}~~~\Leftrightarrow~~~ \ln|y|=-\ln |x|+\ln C\\ \\ \ln|y|=\ln\left|\frac{C}{x}\right|\\ \\ \\ y=\dfrac{C}{x}$