Вспомним формулу для разложения функции в ряд Тейлора
1 Запишем функцию
2 Найдем несколько производных:
...
3 Найдем общий вид производной:
У нас в любом случае будет производная произведения, тогда наша производная распадется на какое-то количество слагаемых либо просто синуса, либо просто косинуса и слагаемое с х умноженным на либо синус, либо косинус.
Заметим, что производная синуса равна
Тогда наше произведение в зависимости от n будет иметь разный вид.
Заметим, что всего различных слагаемых без множителя х будет n штук и все они будут иметь одинаковый знак
И по содержанию, и по знаку наши функции будут одинаковые. Осталось посчитать этот знак.
При n одинаковой четности знак один и тот же, в данной точке функция имеет вид
(производная меняет местами функции)
Мы можем записать для четных n знак у функции в виде где i - мнимая единица, для нечетных n знак тоже можно записать в виде ее степени
Для функции без множителя х формула такая (учитывая значения) - мы должны будем еще умножить на степень для нечетных и также умножить на n (n раз брали производную)
Для функции со множителем формула другая
Чтобы избавится от ненужных двоек в первом случае, умножим все на , и для того, чтобы все осталось как прежде во 2 случае, умножим только его часть на 2
Тогда общая формула производной имеет вид
Можем вынести множитель за скобки
4 Тогда запишем ряд Тейлора
Начинаю с 1 так как писалась формула производной от 1.
а)ε= √21/5 ; A(–5;0)
a=5
ε=c/a
c=ε·a=√21
b2=a2–c2=25–21=4
О т в е т.
(x2/25)+(y2/4)=1
б)A (√80;3) ,B(4 √6 ;3 √2)
Каноническое уравнение гиперболы
(x2/a2)–(y2/b2)=1
чтобы найти а и b подставляем координаты точек А и В:
{(80/a2)–(9/b2)=1
{(96/a2)–(18/b2)=1
Умножаем первое уравнение на (–2):
{–(160/a2)+(18/b2)=–2
{(96/a2)–(18/b2)=1
Складываем
–64/a2=–1
a2=64
18/b2=(96/a2)–1
b2=36
О т в е т. (x2/64)–(y2/36)=1
в)D: y=1
если каноническое уравнение параболы имеет вид
x2=–2py, то фокус параболы
F(0;–p/2)
D: y=p/2
Значит,
p/2=1
p=2
О т в е т. x2=–4y
Пошаговое объяснение:
или проще
Пошаговое объяснение:
Вспомним формулу для разложения функции в ряд Тейлора
1 Запишем функцию
2 Найдем несколько производных:
...
3 Найдем общий вид производной:
У нас в любом случае будет производная произведения, тогда наша производная распадется на какое-то количество слагаемых либо просто синуса, либо просто косинуса и слагаемое с х умноженным на либо синус, либо косинус.
Заметим, что производная синуса равна
Тогда наше произведение в зависимости от n будет иметь разный вид.
Заметим, что всего различных слагаемых без множителя х будет n штук и все они будут иметь одинаковый знак
При n одинаковой четности знак один и тот же, в данной точке функция имеет вид
(производная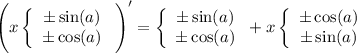 меняет местами функции)
меняет местами функции)
Мы можем записать для четных n знак у функции в виде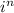 где i - мнимая единица, для нечетных n знак тоже можно записать в виде ее степени
где i - мнимая единица, для нечетных n знак тоже можно записать в виде ее степени 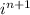
Для функции без множителя х формула такая (учитывая значения)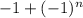 - мы должны будем еще умножить на степень для нечетных и также умножить на n (n раз брали производную)
- мы должны будем еще умножить на степень для нечетных и также умножить на n (n раз брали производную)
Для функции со множителем формула другая
Чтобы избавится от ненужных двоек в первом случае, умножим все на , и для того, чтобы все осталось как прежде во 2 случае, умножим только его часть на 2
, и для того, чтобы все осталось как прежде во 2 случае, умножим только его часть на 2
Тогда общая формула производной имеет вид
Можем вынести множитель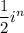 за скобки
за скобки
4 Тогда запишем ряд Тейлора
Начинаю с 1 так как писалась формула производной от 1.
f(2) = 2 * cos ( 2-2 ) = 2 * 1 = 2
Это и есть ответ