Якщо всі бічні грані піраміди однаково нахилені до площини основи, то висота піраміди проходить через…

Якщо всі бічні грані піраміди однаково нахилені до площини основи, то висота піраміди проходить ч

Показать ответ

Ответ:

Luky4anovadasha

20.07.2021 23:06

Формула площади трапеции через стороны (вывод ниже):

$S=\frac{b+d}{2} \sqrt{a^2-\left( \frac{a^2 -c^2+(d-b)^2}{2(d-b)} \right) ^2}$

$S= \frac{8+33}{2}\cdot\sqrt{15^{2}-\left(\frac{15^{2}-20^{2}+\left(33-8\right)^{2}}{2\left(33-8\right)}\right)^{2}} = \\= \frac{41}{2}\cdot\sqrt{225-\left(\frac{225-400+625}{50}\right)^{2}}=\\= \frac{41}{2}\cdot\sqrt{225-\left(\frac{450}{50}\right)^{2}} = \frac{41}{2}\cdot\sqrt{225-81}} = \frac{41}{2}\cdot 12 = 41\cdot 6 =246 \\\\S=246 \:\: (cm^2)$

Объем прямой призмы равен произведению площади основания S на высоту призмы h:

$V= S\cdot h\\ V = 246\cdot 15 = 3690\\ \\ V = 3690 \:\: (cm^3)$

ответ: Объем призмы равен 3690 см³.

_______________________________

Вывести формулу, для того чтобы вычислить площадь трапеции через стороны, можно с метода подстановки.

Проведя две высоты в трапеции, получаем по бокам прямоугольные треугольники с известными гипотенузами и неизвестными катетами x и y. Таким образом x+y = d−b, y = d−b−x.

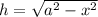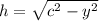Одинаковый катет у обоих треугольников – высота, которую мы ищем. Через теорему Пифагора в прямоугольных треугольниках выражаем высоту $h=\sqrt{a^2-x^2}$ и $h=\sqrt{c^2-y^2}$ . Приравнивая, получаем:

a²−x² = c²−y² или x²−y² = a²−c².

Подставляем вместо х полученное выше выражение d−b−x:

x²−(d−b−x)² = a²−c²

x²−d²+bd+dx-b²+bd−bx−x²+dx−bx = a²−c²

x²−d²+2bd+2dx−b²−2bx−x² = a²−c²

2dx−2bx = a²−c²+d²+b²−2bd

2x(d−b)=a²−c²+(d−b)²

$x=\frac{a^2-c^2+(d-b)^2}{2(d-b)}$

Подставляем обратно x в формулу высоты:

$h=\sqrt{a^2-\left( \frac{a^2 -c^2+(d-b)^2}{2(d-b)} \right) ^2}$

Формула площади трапеции через стороны будет выглядеть так:

$S=\frac{b+d}{2} \sqrt{a^2-\left( \frac{a^2 -c^2+(d-b)^2}{2(d-b)} \right) ^2}$

Основанием прямой призмы является трапеция с основаниями 8 см и 33 см и боковыми сторонами 15 см и 2

0,0(0 оценок)

Ответ:

ksysha98090909

13.11.2022 10:19

Желаю удачи!!:

Пусть скорость автобуса равна х км/ч, а скорость легковой машины - у км/ч. По условию, y - x = 12. Тогда время затраченное автобусом равно , а легковым автомобилем - на весь путь время затрачено часов. Зная, что легковая машина пришла в город В на 5 мин раньше, чем автобус, составим систему уравнений

Умножив левую и правую части уравнения на 3x(x+12) ≠ 0.

По теореме Виета

— не удовлетворяет условию

км/ч — скорость автобуса

Скорость легкового автомобиля: 60 + 12 = 72 км/ч.

ответ: 60 км/ч и 72 км/ч.

0,0(0 оценок)

Популярные вопросы: Математика