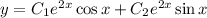1) Y - центральный и X - вписанный углы
Центральный угол равен дуге на которую он опирается, вписанный же половине
X=60 градусов, Y=120 градусов
2) синус угла равен отношению противолежащей стороны к гипотенузе, из рисунка это отношение 3/5=0,6
3) По равенству сторон заметно что искоемое значение является средней линией треугольника, а так как средняя линяя равна половине основания, то x=4
4) Это египетский треугольник со сторонами 3 4 5, x=4
Можно найти по теореме пифагора a^2=c^2-b^2= 25 - 9 = 16, откуда x=4
5) Площадь параллелограмма равна произведению основания на высоту, проведенную к нему S=ah=3*8=24
6) Противоположные углы параллелограмма равны, откуда Y=54 градуса
X = (360-54*2)/2 = 126
7) Обе стороны меньше соотвествующих вдважды 12/6=2 8/4=2, коэффециент подобия равен 2
8) Это параллелограмм, противоположные углы равны, значит 150, остальные два угла 180-150=30
По рисунку видно, что x половина угла x=30/2=15
Вторая часть
1) Радиус описанной окружности равен R=abc/4S из формулы площади треугольника через радиус вписанной окружности S=abc/4R
Найдем гипотенузу по формуле Пифагора c^2=a^2+b^2=144+256=400, откуда c=20
R= (20*16*12) / ( 4 * 0,5 * 12 * 16) = 10, ответ Б
2) Пусть x меньшая, 3x большая сторона, периметр палллелограмма равен P=2ab
2*(3x+x)=60
8x=60 x=7,5 3x=22,5, ответ Б
3) составим уравнение, пусть x неизвестный катет, x+8 гипотенуза. По теореме Пифагора:
20^2 + x^2 = (x+8)^2
400 + x^2 = x^2 + 16x + 64
16x = 336
x=21 x+8=29
P = 20+21+29 = 70, ответ В
4) пусть диагональ BD=12, диагональ AC=4√3
Диагонали ромба деляет его на 4 прямоугольных треугольника, при этом катеты равны половине диагоналей и гипотенуза равна стороне ромба.
BO=OD=6
AO=OC=2√3
AB^2=AO^2+OB^2=36+12=48=4√3
AO=1/2AB ⇒ угол ABO=30 градусов, а угол BAO=180-90-30=60
тогда угол B=2ABO=30*2=60, а угол A=2BAO=60*2=120
Рівняння вигляду де — задані числа, є лінійним однорідним диференціальним рівнянням (ЛОДР) другого порядку зі сталими коефіцієнтами.
Метод Ейлера (метод характеристичних рівнянь) дозволяє знаходити загальний розв'язок для вказаного рівняння.
Розв'язок цього рівняння шукаємо у вигляді де — деяка стала (дійсна чи комплексна). Тоді, якщо то
— характеристичне рівняння
Можливі три випадки:
➀ і — дійсні,
Фундаментальна система розв'язків: — функції лінійно незалежні, бо
Загальний розв'язок:
Приклад: а)
Метод Ейлера:
Характеристичне рівняння:
Відповідь:
Приклад: в)
➁ і — дійсні,
Якщо покласти , то ці функції лінійно залежні, бо
➂ і — комплексно спряжені,
Приклад: б)
Отже,
1) Y - центральный и X - вписанный углы
Центральный угол равен дуге на которую он опирается, вписанный же половине
X=60 градусов, Y=120 градусов
2) синус угла равен отношению противолежащей стороны к гипотенузе, из рисунка это отношение 3/5=0,6
3) По равенству сторон заметно что искоемое значение является средней линией треугольника, а так как средняя линяя равна половине основания, то x=4
4) Это египетский треугольник со сторонами 3 4 5, x=4
Можно найти по теореме пифагора a^2=c^2-b^2= 25 - 9 = 16, откуда x=4
5) Площадь параллелограмма равна произведению основания на высоту, проведенную к нему S=ah=3*8=24
6) Противоположные углы параллелограмма равны, откуда Y=54 градуса
X = (360-54*2)/2 = 126
7) Обе стороны меньше соотвествующих вдважды 12/6=2 8/4=2, коэффециент подобия равен 2
8) Это параллелограмм, противоположные углы равны, значит 150, остальные два угла 180-150=30
По рисунку видно, что x половина угла x=30/2=15
Вторая часть
1) Радиус описанной окружности равен R=abc/4S из формулы площади треугольника через радиус вписанной окружности S=abc/4R
Найдем гипотенузу по формуле Пифагора c^2=a^2+b^2=144+256=400, откуда c=20
R= (20*16*12) / ( 4 * 0,5 * 12 * 16) = 10, ответ Б
2) Пусть x меньшая, 3x большая сторона, периметр палллелограмма равен P=2ab
2*(3x+x)=60
8x=60 x=7,5 3x=22,5, ответ Б
3) составим уравнение, пусть x неизвестный катет, x+8 гипотенуза. По теореме Пифагора:
20^2 + x^2 = (x+8)^2
400 + x^2 = x^2 + 16x + 64
16x = 336
x=21 x+8=29
P = 20+21+29 = 70, ответ В
4) пусть диагональ BD=12, диагональ AC=4√3
Диагонали ромба деляет его на 4 прямоугольных треугольника, при этом катеты равны половине диагоналей и гипотенуза равна стороне ромба.
BO=OD=6
AO=OC=2√3
AB^2=AO^2+OB^2=36+12=48=4√3
AO=1/2AB ⇒ угол ABO=30 градусов, а угол BAO=180-90-30=60
тогда угол B=2ABO=30*2=60, а угол A=2BAO=60*2=120
Рівняння вигляду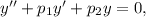 де
де 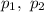 — задані числа, є лінійним однорідним диференціальним рівнянням (ЛОДР) другого порядку зі сталими коефіцієнтами.
— задані числа, є лінійним однорідним диференціальним рівнянням (ЛОДР) другого порядку зі сталими коефіцієнтами.
Метод Ейлера (метод характеристичних рівнянь) дозволяє знаходити загальний розв'язок для вказаного рівняння.
Розв'язок цього рівняння шукаємо у вигляді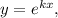 де
де 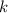 — деяка стала (дійсна чи комплексна). Тоді, якщо
— деяка стала (дійсна чи комплексна). Тоді, якщо 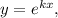 то
то 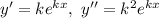
Можливі три випадки:
➀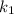 і
і 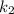 — дійсні,
— дійсні, 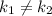
Фундаментальна система розв'язків: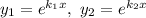 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 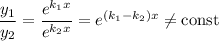
Загальний розв'язок: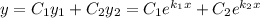
Приклад: а)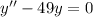
Метод Ейлера: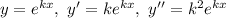
Характеристичне рівняння: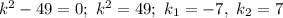
Загальний розв'язок: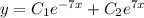
Відповідь: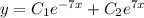
Приклад: в)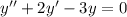
Метод Ейлера: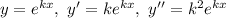
Характеристичне рівняння: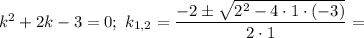
Загальний розв'язок: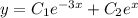
Відповідь: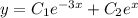
➁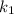 і
і 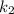 — дійсні,
— дійсні, 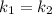
Якщо покласти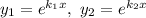 , то ці функції лінійно залежні, бо
, то ці функції лінійно залежні, бо 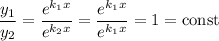
Фундаментальна система розв'язків: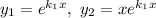 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 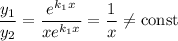
Загальний розв'язок: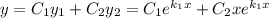
➂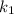 і
і 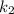 — комплексно спряжені,
— комплексно спряжені, 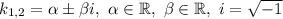
Фундаментальна система розв'язків: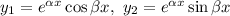 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 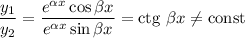
Загальний розв'язок: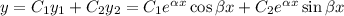
Приклад: б)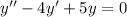
Метод Ейлера: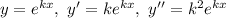
Характеристичне рівняння: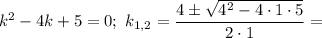
Отже,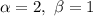
Загальний розв'язок: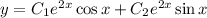
Відповідь: