а - длина прямоугольника b - ширина прямоугольника ================================================================= Р=24 см S=32 см² а - ? см b - ? см Решение: (1)
(2)
из формулы площади прямоугольника (2) выводим формулу нахождения ширины
подставляем в формулу периметра прямоугольника (1)
/·a
умножаем на а для того, чтобы избавиться от знаменателя
подставим в уравнение данные P и S
Квадратное уравнение имеет вид:
Считаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
Следовательно, стороны равны 8см и 4см соответственно
ответ: 8см и 4см стороны прямоугольника. Проверка: Р=2(а+b)=2(8+4)=2·12=24 (см) S=a·b=8·4=32 (м²)
а - длина прямоугольника b - ширина прямоугольника ================================================================= Р=24 см S=32 см² а - ? см b - ? см Решение: (1)
(2)
из формулы площади прямоугольника (2) выводим формулу нахождения ширины
подставляем в формулу периметра прямоугольника (1)
/·a
умножаем на а для того, чтобы избавиться от знаменателя
подставим в уравнение данные P и S
Квадратное уравнение имеет вид:
Считаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
Следовательно, стороны равны 8см и 4см соответственно
ответ: 8см и 4см стороны прямоугольника. Проверка: Р=2(а+b)=2(8+4)=2·12=24 (см) S=a·b=8·4=32 (м²)
а - длина прямоугольника
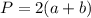 (1)
(1)
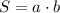 (2)
(2)
b - ширина прямоугольника
=================================================================
Р=24 см
S=32 см²
а - ? см
b - ? см
Решение:
из формулы площади прямоугольника (2) выводим формулу нахождения ширины
подставляем в формулу периметра прямоугольника (1)
умножаем на а для того, чтобы избавиться от знаменателя
подставим в уравнение данные P и S
Квадратное уравнение имеет вид:
Считаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
Следовательно, стороны равны 8см и 4см соответственно
ответ: 8см и 4см стороны прямоугольника.
Проверка:
Р=2(а+b)=2(8+4)=2·12=24 (см)
S=a·b=8·4=32 (м²)
а - длина прямоугольника
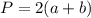 (1)
(1)
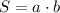 (2)
(2)
b - ширина прямоугольника
=================================================================
Р=24 см
S=32 см²
а - ? см
b - ? см
Решение:
из формулы площади прямоугольника (2) выводим формулу нахождения ширины
подставляем в формулу периметра прямоугольника (1)
умножаем на а для того, чтобы избавиться от знаменателя
подставим в уравнение данные P и S
Квадратное уравнение имеет вид:
Считаем дискриминант:
Дискриминант положительный
Уравнение имеет два различных корня:
Следовательно, стороны равны 8см и 4см соответственно
ответ: 8см и 4см стороны прямоугольника.
Проверка:
Р=2(а+b)=2(8+4)=2·12=24 (см)
S=a·b=8·4=32 (м²)