Сделав один шаг, робот удалится на расстояние , т.к. он идет на 2 м в одном направлении, а потом на 1 м в другом направлении, то соединив точки старта и финиша получаем прямоугольный треугольник с катетами 2 и 1. По теореме Пифагор вычисляем длину гипотенузы, т.е. расстояние, на которое робот удалился от точки старта.
Рассмотрим случаи, когда робот делает два шага (смотри рисунок).
Пусть первый "шаг" он делает вправо и вверх. Второй тоже вправо и вверх. Также соединяем точку старта и финиша и достраиваем до прямоугольного треугольника. Получаем прямоугольный треугольник с катетами 4 и 2. По теореме Пифагора вычисляем длину гипотенузы, т.е. расстояния, на которое робот удалится от точки старта:
Если робот первый шаг сделал вправо и вверх, а второй вправо и вниз, то от точки старта он удалился на 4 м. Это меньше, чем
Если робот первый шаг сделал вправо и вверх, а затем вверх и вправо, то, соединив точки старта и финиша и достроив до прямоугольного треугольника, получим прямоугольный треугольник с катетами 3 и 3.
Длина гипотенузы:
Это тоже меньше, чем
Другие варианты двух "шагов" робота смотри на рисунке.
Из всех вариантов видим, что на наибольшее расстояние робот удаляется тогда, когда идет "лесенкой".
Выстраиваем путь робота "лесенкой". Делаем 5 шагов.
Соединяем точки старта и финиша. Достраиваем полученный отрезок до прямоугольного треугольника (см. рисунок №1). По теореме Пифагора находим длину гипотенузы.
Это и будет наибольшее расстояние, на которое робот удалится за 5 шагов.
ответ:
Задача № 2.
Один из вариантов перемещения в точку, полученную из данной путем перемещения на 8 м в одном направлении и на 14 м в перпендикулярном направлении представлен на рисунке № 2.
Робот делает 8 "шагов" и оказывается в нужной точке.
Вывод: робот может за 8 "шагов" попасть в нужную точку.
Задача 3.
Откладываем 30 м в одном направлении и 24 м в перпендикулярном ему направлении. Соединяем первоначальную точку и точку, получившуюся путем перемещения.
Получаем отрезок.
Этот отрезок и будет кратчайшим расстоянием между точками старта и финиша (на рисунке № 3 он выделен красной пунктирной линией).
Путь робота должен быть максимально приближен к этому отрезку, чтобы он сделал наименьшее количество шагов.
Выстраиваем путь робота так, чтобы точка старта и финиша каждого шага была максимально приближена к отрезку. При этом робот должен идти только веред. Движение назад или отклонение в сторону увеличит количество "шагов".
Считаем количество сделанных "шагов" и получаем ответ: 18 "шагов".
Пусть а - цифра в разряде десятков b- цифра в разряде единиц.
a и b могут принимать только целые значения и только от 0 до 9. Тогда задуманное число можно записать так: 10а + b.
Если цифры задуманного числа поменять местами, то получим: 10b + a.
Разность чисел: 10a + b - (10b + a)
Произведение чисел задуманного числа: a•b
Уравнение 10b + a = 34 + ab 10b - ab = 34 - b b • (10 - a) = 34 - a b = (34 - a) / (10 - a)
Займемся подбором числа a ( как мы помним, от 0 до 9) так, чтобы число b также оказалось любой цифрой от 0 до 9:
а = 1 => b = (34 - 1) / (10 - 1) = 33/9 - не целое
a = 2 =k> b = (34 - 2) / (10 - 2) = 32/8 = 4
а = 3 => b = (34 - 3) / (10 - 3) = 31/7 - не целое
a = 4 => b = (34 - 4) / (10 - 4) = 30/6 = 5
a = 5 => b = (34 - 5) / (10 - 5) = 29/5 - не целое
a = 6 => b = (34 - 6) / (10 - 6) = 28/4 = 7
a = 7 => b = (34 - 7) / (10 - 7) = 27/3 = 9
a = 8 => b = (34 - 8) / (10 - 8) = 26/2 = 13 - это число больше 9
a = 9 => b = (34 - 9) / (10 - 9) = 25/1 = 25 - это число больше 9
Составим таблицу сочетаний целых чисел а и b, но не больших, чем 9: а | b | 10a+b - задуманное число —————————————————— 2 | 4 | 24 4 | 5 | 45 6 | 7 | 67 7 | 9 | 79
ответ: задуманное число может принимать значения: 24; 45; 67 или 79.
Решу эти задачи графически.
Задача № 1.
Сделав один шаг, робот удалится на расстояние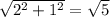 , т.к. он идет на 2 м в одном направлении, а потом на 1 м в другом направлении, то соединив точки старта и финиша получаем прямоугольный треугольник с катетами 2 и 1. По теореме Пифагор вычисляем длину гипотенузы, т.е. расстояние, на которое робот удалился от точки старта.
, т.к. он идет на 2 м в одном направлении, а потом на 1 м в другом направлении, то соединив точки старта и финиша получаем прямоугольный треугольник с катетами 2 и 1. По теореме Пифагор вычисляем длину гипотенузы, т.е. расстояние, на которое робот удалился от точки старта.
Рассмотрим случаи, когда робот делает два шага (смотри рисунок).
Пусть первый "шаг" он делает вправо и вверх. Второй тоже вправо и вверх. Также соединяем точку старта и финиша и достраиваем до прямоугольного треугольника. Получаем прямоугольный треугольник с катетами 4 и 2. По теореме Пифагора вычисляем длину гипотенузы, т.е. расстояния, на которое робот удалится от точки старта: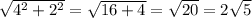
Если робот первый шаг сделал вправо и вверх, а второй вправо и вниз, то от точки старта он удалился на 4 м. Это меньше, чем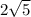
Если робот первый шаг сделал вправо и вверх, а затем вверх и вправо, то, соединив точки старта и финиша и достроив до прямоугольного треугольника, получим прямоугольный треугольник с катетами 3 и 3.
Длина гипотенузы: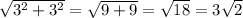
Это тоже меньше, чем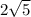
Другие варианты двух "шагов" робота смотри на рисунке.
Из всех вариантов видим, что на наибольшее расстояние робот удаляется тогда, когда идет "лесенкой".
Выстраиваем путь робота "лесенкой". Делаем 5 шагов.
Соединяем точки старта и финиша. Достраиваем полученный отрезок до прямоугольного треугольника (см. рисунок №1). По теореме Пифагора находим длину гипотенузы.
Это и будет наибольшее расстояние, на которое робот удалится за 5 шагов.
ответ: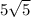
Задача № 2.
Один из вариантов перемещения в точку, полученную из данной путем перемещения на 8 м в одном направлении и на 14 м в перпендикулярном направлении представлен на рисунке № 2.
Робот делает 8 "шагов" и оказывается в нужной точке.
Вывод: робот может за 8 "шагов" попасть в нужную точку.
Задача 3.
Откладываем 30 м в одном направлении и 24 м в перпендикулярном ему направлении. Соединяем первоначальную точку и точку, получившуюся путем перемещения.
Получаем отрезок.
Этот отрезок и будет кратчайшим расстоянием между точками старта и финиша (на рисунке № 3 он выделен красной пунктирной линией).
Путь робота должен быть максимально приближен к этому отрезку, чтобы он сделал наименьшее количество шагов.
Выстраиваем путь робота так, чтобы точка старта и финиша каждого шага была максимально приближена к отрезку. При этом робот должен идти только веред. Движение назад или отклонение в сторону увеличит количество "шагов".
Считаем количество сделанных "шагов" и получаем ответ: 18 "шагов".
ответ: 18
b- цифра в разряде единиц.
a и b могут принимать только целые значения и только от 0 до 9.
Тогда задуманное число можно записать так:
10а + b.
Если цифры задуманного числа поменять местами, то получим:
10b + a.
Разность чисел:
10a + b - (10b + a)
Произведение чисел задуманного числа:
a•b
Уравнение
10b + a = 34 + ab
10b - ab = 34 - b
b • (10 - a) = 34 - a
b = (34 - a) / (10 - a)
Займемся подбором числа a ( как мы помним, от 0 до 9) так, чтобы число b также оказалось любой цифрой от 0 до 9:
а = 1 => b = (34 - 1) / (10 - 1) = 33/9 - не целое
a = 2 =k> b = (34 - 2) / (10 - 2) = 32/8 = 4
а = 3 => b = (34 - 3) / (10 - 3) = 31/7 - не целое
a = 4 => b = (34 - 4) / (10 - 4) = 30/6 = 5
a = 5 => b = (34 - 5) / (10 - 5) = 29/5 - не целое
a = 6 => b = (34 - 6) / (10 - 6) = 28/4 = 7
a = 7 => b = (34 - 7) / (10 - 7) = 27/3 = 9
a = 8 => b = (34 - 8) / (10 - 8) = 26/2 = 13 - это число больше 9
a = 9 => b = (34 - 9) / (10 - 9) = 25/1 = 25 - это число больше 9
Составим таблицу сочетаний целых чисел а и b, но не больших, чем 9:
а | b | 10a+b - задуманное число
——————————————————
2 | 4 | 24
4 | 5 | 45
6 | 7 | 67
7 | 9 | 79
ответ: задуманное число может принимать значения: 24; 45; 67 или 79.