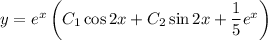... Я был в его группе Pascaly, которые дают представления в Черновцах. Еминеску, суфлер, с некоторыми пешеходных ботинках разбитых в горе им кое-какую одежду. И он заметил, Pascaly директор. -Я Замечание? -Нет. Я спросил, если он не имеет ничего лучше. Я ответил, что поэт имеет. -Ну, Купить ваши ... - Чтобы купить мне ... Но я пятаков. -Poftim Пятьдесят леев ... Позволь мне жить сегодня с обувью и одеждой! Вы понимаете? -Я Поймите, ответил Эминеску, которые берут деньги и покинуть город. Когда он вернулся вечером, я беру короткий Pascaly: Вы купили одежду и ботинки, сэр? Да! -Где? -Look Их. И дал полное собрание сочинений Гете и Гейне. Посмотрите, сапоги и одежда ... Дополнен 4 года назад
Это была красота! Классический рисунок, обрамленный какой-нибудь большой волосатая, черная. Высокий лоб и безмятежный, некоторые крупные глаза ...- окна души; ... Нежный улыбка и глубокую меланхолию. Он имел вид молодого святого, происходил из древней иконой, ребенок предопределил боли, которые видят надпись на лице будущей мучений. -Я Рекомендуют Михая Эминеску! Так что я знал, я ...
Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами, общим решением которого является .
1) — общее решение соответствующего линейного однородного дифференциального уравнения:
Применим метод Эйлера: сделаем замену где — некоторая постоянная. Тогда
Получили характеристическое уравнение:
Разделим обе части уравнения на :
Отрицательный дискриминант означает, что корни данного уравнения будут комплексно-сопряженными:
Тогда
Воспользуемся формулой Эйлера:
Фундаментальная система решений: — функции линейно независимые, поскольку
Общее решение:
2) — частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции .
Здесь , причем , поэтому частное решение имеет вид , где — неизвестный коэффициент, который нужно найти.
Тогда и подставим в исходное ЛНДР и найдем :
Разделим обе части уравнения на
Таким образом, частное решение:
Тогда общим решением исходного ЛНДР с постоянными коэффициентами:
Это была красота! Классический рисунок, обрамленный какой-нибудь большой волосатая, черная. Высокий лоб и безмятежный, некоторые крупные глаза ...- окна души; ... Нежный улыбка и глубокую меланхолию. Он имел вид молодого святого, происходил из древней иконой, ребенок предопределил боли, которые видят надпись на лице будущей мучений. -Я Рекомендуют Михая Эминеску! Так что я знал, я ...
Имеем линейное неоднородное дифференциальное уравнение второго порядка с постоянными коэффициентами, общим решением которого является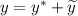 .
.
1)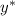 — общее решение соответствующего линейного однородного дифференциального уравнения:
— общее решение соответствующего линейного однородного дифференциального уравнения:
Применим метод Эйлера: сделаем замену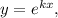 где
где 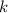 — некоторая постоянная. Тогда
— некоторая постоянная. Тогда 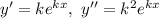
Получили характеристическое уравнение:
Разделим обе части уравнения на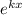 :
:
Отрицательный дискриминант означает, что корни данного уравнения будут комплексно-сопряженными:
Тогда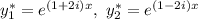
Воспользуемся формулой Эйлера: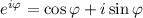
Фундаментальная система решений: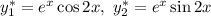 — функции линейно независимые, поскольку
— функции линейно независимые, поскольку 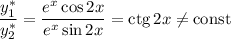
Общее решение: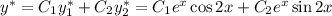
2)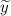 — частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции
— частное решение линейного неоднородного дифференциального уравнения, которое находится с метода подбора вида частного решения по виду правой части функции 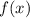 .
.
Здесь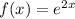 , причем
, причем 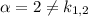 , поэтому частное решение имеет вид
, поэтому частное решение имеет вид 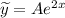 , где
, где 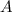 — неизвестный коэффициент, который нужно найти.
— неизвестный коэффициент, который нужно найти.
Тогда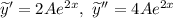 и
и 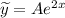 подставим в исходное ЛНДР и найдем
подставим в исходное ЛНДР и найдем 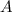 :
:
Разделим обе части уравнения на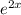
Таким образом, частное решение: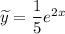
Тогда общим решением исходного ЛНДР с постоянными коэффициентами:
ответ: