Математика: За неправильный ответ забаню))

За неправильный ответ забаню))

Показать ответ

Ответ:

Kira1574

14.04.2021 18:35

1. 3x⁴ + 3x³ – 8x² – 2x + 4 = 0

Попробуем найти корни подбором, проверим все целые x в интервале [–3; 3]. Корнями являются значения x = –2 и x = 1, поэтому многочлен (3x⁴ + 3x³ – 8x² – 2x + 4) делится на (x + 2)(x – 1) = x² + x – 2.

Поделим (3x⁴ + 3x³ – 8x² – 2x + 4) на (x² + x – 2), см. рисунок с делением многочленов столбиком: 3x⁴ + 3x³ – 8x² – 2x + 4 = (x + 2)(x – 1)(3x² – 2). Разложим (3x² – 2) на множители: 3x² – 2 = 3(x² – 2/3) = 3(x – √(2/3))(x + √(2/3)).

Таким образом, исходное уравнение равносильно уравнению 3(x + 2)(x – 1)(x – √(2/3))(x + √(2/3)) = 0, корнями которого являются значения x₁ = –2, x₂ = 1, x₃ = –√(2/3), x₄ = √(2/3).

ответ: x₁ = –2, x₂ = 1, x₃ = –√(2/3), x₄ = √(2/3).

2. Пределы можно найти, воспользовавшись правилом Лопиталя-Бернулли: предел отношения функций, стремящихся одновременно к бесконечности или к нулю, равен пределу отношения их производных.

В первом примере достаточно продифференцировать один раз, потому что после этого числитель и знаменатель перестают стремиться к бесконечности или к нулю:

$\lim_{x\to4}\dfrac{x^3-64}{x^2-16} = \lim_{x\to4}\dfrac{(x^3-64)'}{(x^2-16)'} = \lim_{x\to4}\dfrac{3x^2}{2x} = \dfrac{3\cdot4^2}{2\cdot4} = \dfrac{48}{8} = 6$

Во втором примере нужно дифференцировать трижды, так как на всех предыдущих шагах и числитель, и знаменатель все еще стремятся к бесконечности:

$\lim_{x\to\infty}\dfrac{x^3+2x-7}{6x^3+4x^2+3} = \lim_{x\to\infty}\dfrac{(x^3+2x-7)'''}{(6x^3+4x^2+3)'''} = \lim_{x\to\infty}\dfrac{(3x^2+2)''}{(18x^2+8x)''} = \lim_{x\to\infty}\dfrac{(6x)'}{(36x+8)'} = \lim_{x\to\infty}\dfrac{6}{36} = \dfrac{1}{6}$

3. Снова воспользуемся правилом Лопиталя-Бернулли:

$\lim_{x\to0}\dfrac{sin(7x)}{tg(3x)} = \lim_{x\to0}\dfrac{(sin(7x))'}{(tg(3x))'} = \lim_{x\to0}\dfrac{7cos(7x)}{3/cos^2(3x)} = \dfrac{7}{3}$

4a. Производная функции: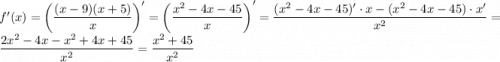 $f'(x) = \left(\dfrac{(x-9)(x+5)}{x}\right)' = \left(\dfrac{x^2-4x-45}{x}\right)' = \dfrac{(x^2-4x-45)'\cdot x-(x^2-4x-45)\cdot x'}{x^2} = \dfrac{2x^2-4x-x^2+4x+45}{x^2} = \dfrac{x^2+45}{x^2}$