Пусть уравнение искомой кривой y=y(x). Рассмотрим произвольную точку на плоскости, производную в этой точке обозначим через Уравнение касательной к кривой будет иметь вид
Чтобы узнать, где эта касательная пересекается с осью OY, подставим x=0:
По условию
Поскольку - произвольная точка, можно последнее условие переписать в виде
Поскольку по условию кривая проходит через точку можем найти C:
И наконец, поскольку абсцисса точки которая лежит на кривой, положительна, и во всех других точках кривой абсцисса будет положительной, поэтому окончательный ответ такой:
Пусть уравнение искомой кривой y=y(x). Рассмотрим произвольную точку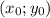 на плоскости, производную в этой точке обозначим через
на плоскости, производную в этой точке обозначим через 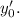 Уравнение касательной к кривой будет иметь вид
Уравнение касательной к кривой будет иметь вид
Чтобы узнать, где эта касательная пересекается с осью OY, подставим x=0:
По условию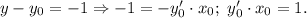
Поскольку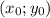 - произвольная точка, можно последнее условие переписать в виде
- произвольная точка, можно последнее условие переписать в виде
Поскольку по условию кривая проходит через точку можем найти C:
можем найти C:
И наконец, поскольку абсцисса точки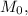 которая лежит на кривой, положительна, и во всех других точках кривой абсцисса будет положительной, поэтому окончательный ответ такой:
которая лежит на кривой, положительна, и во всех других точках кривой абсцисса будет положительной, поэтому окончательный ответ такой: