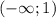Задача: Щорічно проводиться посадка ялинок у спеціальних розплідниках для продажу на новорічні свята.
1)Ділянка, на якій буде висаджено ялинки, дорівнює 2368м². її ширина на 42м менша за довжину. знайдіть ширину та довжину ділянки для посадки дерев. Скільки соток становить дана ділянка?
2)Висаджують молоді саджанці ялинки у підготовлений, проріджений грунт на відстані двох метрів
один від одного. Яку кількість посаджених дерев буде висаджено на даній ділянці?
3)Обчисліть, скільки кубічних метрів повітря очистить дана посадка ялинок від вихлопних газів. Відомо, що одне дерево очищує зону довжиною 100метрів, шириною 8метрів і висотою 12метрів

​

нет не может. Потому как целое число , дилимое на 8, найболее приближенное к числу 225 является число 224. Чтоб получить число 224 нужно чтоб на всех кустах расло поровну 28 ягод. А поскольку количество ягод на соседних кустах отличается на 1, то и градация разници ягод будет в пределах 4 ягод.Например:

28  27  28  27  28  27  28  27  (4 единицы не хватает)

28  29  28  29  28  29  28  29  (4 единицы в избытке)

А для верности условия градация количества ягод не должна превышать 1 , так как 225-224=1.

Не может на всех кустах вместе расти 225 ягод.

a)f(x)=-8x^2-2x+1

f'(x)=-8*2x-2*1=-16x-2

-16x-2>0

-16x>2

x<-2/16

x<-1/8

b)f(x)=1+x-6x^2

f'(x)=1-6*2x=1-12x

1-12x>0

-12x>-1

12x<1

x<1/12

c)f(x)=(x^3/3)-(x^2)+2

f'(x)=1/3 * 3x^2 -2*x=x^2 - 2x

x^2 - 2x>0

x^2 - 2x =0

x(x-2)=0

x=0   x=2

Чертим координатную прямую и отмечаем точки, расставляем знаки.

___+______-______+_____

           0            2

Решением неравенства является промежуток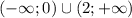

d)f(x)=((-x^3)/3)- 1/2x^2+6/7

f'(x)=-1/3 * 3x^2 - 1/2 * (-2)* 1/x^3 =-x^2 +1/x^3

-x^2 + 1/x^3 >0

Домножим на  x^3:

-x^5 +1>0

-x^5>-1

x^5 < 1

x<1

Решением будет являться промежуток