Математика: Задание на картинке заранее

Для более удобного нахождения значений тригонометрических функций, которые принимают вид или , , используют формулы приведения, где , — некий острый угол.Если тригонометрическая функция имеет вид , то название тригонометрической функции не меняется и она принимает вид с учетом знака четверти, в которой находится значение для данной функции.Если тригонометрическая функция имеет вид , то название тригонометрической функции меняется на кофункцию (то есть на ту же самую функцию с добавлением или убиранием...

Задание на картинке заранее

Показать ответ

Ответ:

saschaalexandrova

27.11.2022 15:15

Пошаговое объяснение:

1) и 2) легкотня.

Тут, насколько я знаю, действует одна фиговина: минус на минус - это ПЛЮС. Попробуй подставь эти числа, при этом, если увидишь, что будет два минуса, превращай это в плюс. Допустим:

-a+b+c-d

1) -(-4)+12-6-8 = 4+12-6-8= 2

2) Аналогично:

-1.5-3.2-1.8-(-2.4) = -4.7-1.8+2.4 = -6.5+2.4 = - 4.1

Если, к примеру, в выражении A отрицательная, а его число положительное, то в итоге будет отрицательное число.

А вот с 3) и 4) немного потяжелее.

Я могу только кратко написать.

Сначала применяешь правило, которое я описал в 1) и 2) (если будет два минуса), подставляешь числа, меняя знаки, потом нужно перевести в неправильную дробь (целое умножить на знаменатель и затем прибавить числитель, если ты не знаешь). После этого приводишь к общему знаменателю, а дальше дело само пойдёт.

0,0(0 оценок)

Ответ:

Kristing15

01.12.2022 19:25

$1. \ \sin 225^{\circ} + \cos 330^{\circ} + \text{ctg} \ 510^{\circ} = \sin (180^{\circ} + 45^{\circ}) + \cos (360^{\circ} - 30^{\circ}) + \\+ \text{ctg} (540^{\circ} - 30^{\circ}) = -\sin 45^{\circ} + \cos 30^{\circ} - \text{ctg} 30^{\circ} = -\dfrac{\sqrt{2}}{2} + \dfrac{\sqrt{3}}{2} - \sqrt{3} = \\= \dfrac{-\sqrt{2} + \sqrt{3} - 2\sqrt{3}}{2} = -\dfrac{\sqrt{2} + \sqrt{3}}{2}$

$2. \ \sin \dfrac{17\pi}{6} + \cos \dfrac{14\pi}{3} - \text{tg} \ \dfrac{13\pi}{4} = \sin \left(3\pi - \dfrac{\pi}{6}\right) + \cos \left(5\pi - \dfrac{\pi}{3}\right) - \\-\text{tg} \left(\dfrac{7\pi}{2} - \dfrac{\pi}{4}\right) = \sin \dfrac{\pi}{6} - \cos \dfrac{\pi}{3} - \text{ctg} \ \dfrac{\pi}{4} = \dfrac{1}{2} - \dfrac{1}{2} -1 = -1$

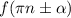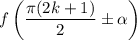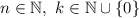Для более удобного нахождения значений тригонометрических функций, которые принимают вид $f(\pi n \pm \alpha )$ или $f\left(\dfrac{\pi (2k+1)}{2} \pm \alpha \right)$ , $n \in \mathbb{N}, \ k \in \mathbb{N} \cup \{0\}$ , используют формулы приведения, где 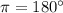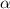$\pi = 180^{\circ}$ , $\alpha$ — некий острый угол.

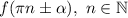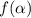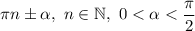Если тригонометрическая функция имеет вид $f(\pi n \pm \alpha ), \ n \in \mathbb{N}$ , то название тригонометрической функции не меняется и она принимает вид $f(\alpha )$ с учетом знака четверти, в которой находится значение $\pi n \pm \alpha, \ n \in \mathbb{N}, \ 0$ для данной функции.

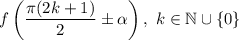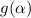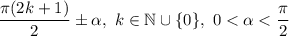Если тригонометрическая функция имеет вид $f\left(\dfrac{\pi (2k+1)}{2} \pm \alpha\right), \ k \in \mathbb{N} \cup \{0\}$ , то название тригонометрической функции меняется на кофункцию (то есть на ту же самую функцию с добавлением или убиранием приставки «ко-») и она принимает вид $g(\alpha )$ с учетом знака четверти, в которой находится значение $\dfrac{\pi (2k+1)}{2} \pm \alpha, \ k \in \mathbb{N} \cup \{0\}, \ 0$ , для функции .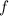