Ранжируем данный ряд (разместим элементы данного ряда в порядке возрастания):
Размах выборки — это разность между наибольшим и наименьшим значениями случайной величины в выборке:
Среднее арифметическое — сумма всех элементов выборки, поделенное на их количество
Сумма элементов выборки:
Количество элементов выборки:
Среднее арифметическое выборки:
Мода — это то значение случайной величины, которое встречается наиболее часто.
Имеем две моды:
Медиана — это так называемое срединное значение упорядоченного ряда значений случайной величины:
— если количество элементов в ряду нечетное, то медиана — это число, записанное посередине;
— если количество элементов в ряду четное, то медиана — это среднее арифметическое двух чисел, стоящих посередине.
В нашем ряду количество элементов четное (8 элементов). Два срединных элемента выборки: и
ответ:
384 × 736 ÷ ( 2 745 - 2 721 ) - ( 5 560 - 1 060 ) ÷ 2 = 9 526
1) 2 745 - 2 721 = 24
2) 5 560 - 1 060 = 4 500
3) 384 × 736 = 282 624
4) 282 624 ÷ 24 = 11 776
5) 4 500 ÷ 2 = 2 250
6) 11 776 - 2 250 = 9 526
( 1 125 + 875 ) × 18 + 4 328 + ( 976 543 - 123 459 ) × 1 = 893 412
1) 1 125 + 875 = 2 000
2) 976 543 - 123 459 = 853 084
3) 2 000 × 18 = 36 000
4) 853 084 × 1 = 853 084
5) 36 000 + 4 328 = 40 328
6) 40 328 + 853 084 = 893 412
2 025 ÷ 15 × ( 524 + 195 ) ÷ 9 + ( 308 308 - 207 207 ) × 2 = 212 987
1) 524 + 195 = 719
2) 308 308 - 207 207 = 101 101
3) 2 025 ÷ 15 = 135
4) 135 × 719 = 97 065
5) 97 065 ÷ 9 = 10 785
6) 101 101 × 2 = 202 202
7) 10 785 + 202 202 = 212 987
Ранжируем данный ряд (разместим элементы данного ряда в порядке возрастания):
Размах выборки — это разность между наибольшим и наименьшим значениями случайной величины в выборке:
— это разность между наибольшим и наименьшим значениями случайной величины в выборке:
Среднее арифметическое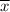 — сумма
— сумма 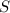 всех элементов выборки, поделенное на их количество
всех элементов выборки, поделенное на их количество 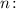
Сумма элементов выборки: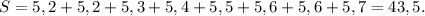
Количество элементов выборки: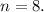
Среднее арифметическое выборки: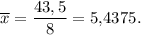
Мода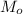 — это то значение случайной величины, которое встречается наиболее часто.
— это то значение случайной величины, которое встречается наиболее часто.
Имеем две моды: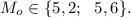
Медиана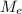 — это так называемое срединное значение упорядоченного ряда значений случайной величины:
— это так называемое срединное значение упорядоченного ряда значений случайной величины:
— если количество элементов в ряду нечетное, то медиана — это число, записанное посередине;
— если количество элементов в ряду четное, то медиана — это среднее арифметическое двух чисел, стоящих посередине.
В нашем ряду количество элементов четное (8 элементов). Два срединных элемента выборки: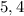 и
и 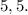
ответ: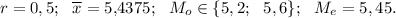
384 × 736 ÷ ( 2 745 - 2 721 ) - ( 5 560 - 1 060 ) ÷ 2 = 9 526
1) 2 745 - 2 721 = 24
2) 5 560 - 1 060 = 4 500
3) 384 × 736 = 282 624
4) 282 624 ÷ 24 = 11 776
5) 4 500 ÷ 2 = 2 250
6) 11 776 - 2 250 = 9 526
( 1 125 + 875 ) × 18 + 4 328 + ( 976 543 - 123 459 ) × 1 = 893 412
1) 1 125 + 875 = 2 000
2) 976 543 - 123 459 = 853 084
3) 2 000 × 18 = 36 000
4) 853 084 × 1 = 853 084
5) 36 000 + 4 328 = 40 328
6) 40 328 + 853 084 = 893 412
2 025 ÷ 15 × ( 524 + 195 ) ÷ 9 + ( 308 308 - 207 207 ) × 2 = 212 987
1) 524 + 195 = 719
2) 308 308 - 207 207 = 101 101
3) 2 025 ÷ 15 = 135
4) 135 × 719 = 97 065
5) 97 065 ÷ 9 = 10 785
6) 101 101 × 2 = 202 202
7) 10 785 + 202 202 = 212 987