Заданы ожидание m и среднее квадратическое отклонение нормально распределённой случайной величины.
требуется найти: а) вероятность того, что x примет значение, принадлежащее интервалу (a, b);
б) вероятность того, что абсолютная величина отклонения |x-m| окажется меньше положительного числа n.
Пошаговое объяснение:
К - середина АА₁,
N - середина ВВ₁,
L - середина A₁D₁.
Соединяем точки N и К, K и L, так как каждая пара лежит в одной грани.
_______________
Отрезок, соединяющий середины противоположных сторон квадрата, параллелен другой паре сторон квадрата и равен стороне квадрата:
В₁N║A₁K так как лежат на противоположных сторонах квадрата,
В₁N = A₁K как половины равных отрезков, ∠NВ₁А₁ = 90°, значит NВ₁А₁K - прямоугольник, ⇒ NK║A₁B₁, NK = A₁B₁.
________________________
KN║A₁B₁ как отрезок, соединяющий середины противоположных сторон квадрата, значит, А₁В₁║(KLN).
Пусть М - середина В₁С₁. Тогда LM║A₁B₁.
Соединяем точки M и N.
KLMN - искомое сечение.
KN║A₁B₁, KN = A₁B₁,
LM║A₁B₁, LM = A₁B₁, значит KLMN - параллелограмм.
A₁L - проекция KL на плоскость (А₁В₁С₁), A₁L⊥A₁B₁, ⇒KL⊥A₁B₁ по теореме о трех перпендикулярах, ⇒
KL ⊥ KN, значит KLMN - прямоугольник.
KN = A₁B₁ = 1, так как куб единичный.
ΔKA₁L: ∠KA₁L = 90°, по теореме Пифагора
Пошаговое объяснение:
Обозначим через K середину ребра AA₁, через N середину ребра BB₁ и через L середину ребра A₁D₁. Так как прямые KL и KN лежат на плоскости сечения, KL||NM и KN||LM, то, следовательно прямая KM также лежит на плоскости сечения. В силу этого площадь S=KN•KL прямоугольника KLMN будет искомой площадью сечения.
Длина KN = 1, LK - гипотенуза в равнобедренном прямоугольном треугольнике KLA₁ с катетом равным 1/2. Применим теорему Пифагора:
KL² = KA₁²+ LA₁² = (1/2)²+(1/2)² = 1/4+1/4 =1/2 или KL=1/√2.
Тогда площадь прямоугольника KLMN, то есть площадь сечения, равна
S = KN•KL = 1•1/√2 =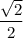 (кв. единица).
(кв. единица).