Записать уравнение прямой, проходящей через точку m(7; -3) с заданным уголовым коэффициентом k=1/2. полученное уравнение к общему виду и в отрезках на осях
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа будет являться число .
В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси ).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.
Первый Так как у ромба длины всех его сторон равны, то треугольник АСД равнобедренный, тогда угол САД = АСД = 570.
Сумма внутренних углов треугольника равна 1800, тогда угол АДС = (180 – 57 – 57) = 660.
У ромба противоположные углы равны, тогда угол АВС = АДС = 660.
Второй Диагонали ромба есть биссектрисы углов при вершинах, тогда угол ВСД = 2 * АСД = 2 * 57 = 1140.
У ромба сумма соседних углов равна 1800, тогда угол АВС = 180 – ВСД = 180 – 114 = 660.
ответ: Угол АВС равен 660.
Пошаговое объяснение:
Пошаговое объяснение:
Точка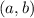
на комплексной плоскости изображает число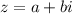 
В соответствии с этим строим точки для 16.1. (Картинка 1)
Комплексно-сопряженные числа — пара комплексных чисел, обладающих одинаковыми действительными частями и равными по абсолютной величине противоположными по знаку мнимыми частями.
Т.е. сопряженным для числа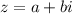
будет являться число 
.
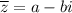В графическом представлении это означает, что сопряженное число будет являться отражением исходного числа относительно действительной оси (оси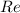
).
На Картинке 2 серым обозначены исходные точки и синим - комплексно-сопряженные с ними.