Математика: Записати відсотки у вигляді відсоткового Дробу:130%

Записати відсотки у вигляді відсоткового Дробу:130%

Показать ответ

Ответ:

Карнова

04.05.2020 05:57

то есть у нас есть 3 события - извлечения первого, второго, третьего пакета молока 1 2 3

нужно чтобы были успешными либо 1 и 2, либо 1 и 3, либо 2 и 3 событие.

посчитаем вероятности, сложим (знаем чтобы узнать вероятность двух идущих друг за другом действий надо перемножить вероятности их выполнения)

(3 / 5) * (2 / 4) * (2 / 3) = 1 / 5

почему именно такие цифры?

3/5 - из пяти пакетов всего(3 из них местные) вытащить 1

2/4 - из оставшихся четырех пакетов(2 из них осталось местных, потому что один мы уже вытващили)

2 / 3 - из трех пакетов(1 из них местный) вытащить не местный пакет

по аналогии делаем оставшиеся два варианта

(3 / 5) * (2 / 4) * (2 / 3) = 1 / 5

и третий случай

(2 / 5) * (3 / 4) * (2 / 3) = 1 / 5

считаем сумму - 3 / 5 = 0,6

ответ вероятность 60%

а вообще лучше почитай теорему умножения вероятностей у зависимых событий, может быть понять(ну и еще во всех трех случаях вероятность одна и та же, это тоже оттуда)

0,0(0 оценок)

Ответ:

SuperSaam

19.08.2022 21:57

Обозначим катеты за a = 9 см, b = 12 см , гипотенузу за c, высоту за h, проекции катетов на гипотенузу за ca и ba.

Исходя из т. Пифагора, следует:

$c^2=a^2+b^2 = c=\sqrt{a^2+b^2} \\c = \sqrt{9^2+12^2}= \sqrt{81+144} = \sqrt{225} = 15 \:\: (cm)$

Найдет площадь прямоугольного треугольника:

$S = \frac{a\cdot b}{2} \\S = \frac{9\cdot 12}{2} = 9\cdot 6 = 54 \:\: (cm^2)$

Воспользуемся формулой площади треугольника через высоту и выразим из нее высоту:

$S = \frac{h\cdot c_h}{2} = 2S = h\cdot c_h = h = \frac{2S}{c_h} \\h = \frac{2\cdot 54}{15} = \frac{108}{15}= 7\frac{3}{15} =7\frac{1}{5}=7,2 \:\: (cm)$

Проекции катетов будут равны:

$ca = \sqrt{a^2-h^2} \\ca = \sqrt{9^2-7,2^2} = \sqrt{81-51,84}= \sqrt{29,16} = 5,4 \:\: (cm) \\\\cb = \sqrt{b^2-h^2} \\cb = \sqrt{12^2-7,2^2} = \sqrt{144-51,84}= \sqrt{92,16} = 9,6 \:\: (cm)$

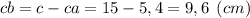
или $cb = c-ca = 15-5,4 = 9,6 \:\: (cm)$

—————————————————————————————

Высоту и проекции катетов также можно найти через пропорциональные отрезки в прямоугольном треугольнике:

– высота, проведенная к гипотенузе, есть среднее пропорциональное между проекциями катетов на гипотенузу:

$h^2 = ca\cdot cb = h=\sqrt{ca\cdot cb}$

– катет есть среднее пропорциональное между гипотенузой и проекцией этого катета на гипотенузу:

$a^2 = ca\cdot c = ca = \frac{a^2}{c} \\b^2 = cb\cdot c = cb = \frac{b^2}{c}\\\\$

—————————————————————————————

$ca=\frac{9^2}{15} = \frac{81}{15} = 5,4 \:\: (cm) \\\\cb=\frac{12^2}{15} = \frac{144}{15} = 9,6 \:\: (cm) \\\\h=\sqrt{5,4\cdot 9,6} =\sqrt{51,84} = 7,2 \:\: (cm)$