Необходимо постоянно вырабатывать уверенность в возможностях управлять своим поведением и поступками, учиться находить оптимальное решение в различных экстремальных ситуациях, жить с собой в согласии; быть оптимистом, помнить, что источником стресса являются не события сами по себе, а наше восприятие этих событий. Как только вы почувствовали, что у вас портится настроение, постарайтесь переключиться на что-то хорошее, на те события, с которыми у вас связаны приятные воспоминания, — это снизит стресс и видеть жизнь в более светлых тонах.Научитесь ставить перед собой посильные задачи, которые вы в состоянии выполнить без перенапряжения. Реально смотрите на свои возможности, не ждите от себя многого, не драматизируйте неудачи, помните, что совершенство в принципе недостижимая вещь.Учитесь радоваться жизни, старайтесь получать хоть маленькие радости от каждого прожитого дня, радуйтесь своим и чужим успехам.
Далее заметим, что для любого верно . То есть верхнее ограничение выполняется автоматически. Значит, полученная задача равносильна задаче о решении уравнения в целых неотрицательных числах.
А для такой задачи применим метод шаров и перегородок: количество решений уравнения (1) совпадает с количеством размещений 4 неразличимых шаров в 9 ящиках [или, что то же самое, с количеством разделения ряда из 4 шаров 8 перегородками].
Пошаговое объяснение:
Введем замену
; 
.
Уравнение примет вид
Далее заметим, что для любого
верно 
. То есть верхнее ограничение 
выполняется автоматически. Значит, полученная задача равносильна задаче о решении уравнения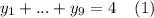 
в целых неотрицательных числах.
А для такой задачи применим метод шаров и перегородок: количество решений уравнения (1) совпадает с количеством размещений 4 неразличимых шаров в 9 ящиках [или, что то же самое, с количеством разделения ряда из 4 шаров 8 перегородками].
Искомое количество вариантов