Усучасному суспільстві є багато людей, які заради грошей здатні на все, вони економлять свої гроші на кожному кроці, і намагаються як найменше їх тратити. але чи можна сказати, що вони скнари, можливо вони “філософи”, які з розумом ставляться до своїх заощаджень і можливо вони посупають правельно. оноре де у свому творі “гобсек” звертає увагу читачів саме на негативному впливі банатства на людей, яке робить з людини істоту без честі й совісті, яка готова піти на все заради свого стану в суспільстві. гобсек- це багата людина ,яка працювала все своє життя лихварем,який був дуже заощадливим і саме так він став мільйонером. але його мільйони не вплинули на спосіб життя чоловіка. увесь час він жив у скромнім і старім будинку. багатство гобсека зробило його самотнім але це не хвилювало його. саме через це у нього немає друзів, сім”ї , родини. йому не відомі звичайні почуття людини, почуття: жалю,кохання, дружби. його єдина любов-це гроші. автор спеціально описує нам його образ,щоб показати нам сутність чоловіка. прочитавши можна зрозуміти,що золото зробило його життя мертвим і холодним, і вбило в ньому усі людські риси в творі придставлено два соціального середовища. це багатії , які розтрачають свої гроші на насолоди і розкоші. і бідні люди, які працювали невіддихаючи, щоб заробити собі на прожиття. і гобсек зрозумів, що саме гроші є головною силою у їхньому суспільстві. своєю пристрастю до грошей чоловік забов”язаний тим людям, які розділили суспільство на дві касти населення: будних і багатих. чоловік був дуже розумним і поставивсобі мету, що краже він задавить багатих ніж вони задавлять його. забираючи кридити у людей гобсек був жорстокий і холодний, саме цим він якав їх. йому те, що від нього були залежні люди вищої касти і він міг керувати ними через гроші. але все ж таки йому були притаманні риси філософа. думається, що йому було непотрібно було усі ці гроші, він жив заради влади над людьми. саме у фіналі жадібність гобсека погубила його він був задоволеним своїм життям я вважаю, що цей чоловік був скоріше філософом, ніж скнарою. багато моментів у творі говорить про його розум і хитрість. йому було непортібні його гроші перш за все він жаждив влади саме через це його варто назвати філософом того часу.
Вспомним формулу для разложения функции в ряд Тейлора
1 Запишем функцию
2 Найдем несколько производных:
...
3 Найдем общий вид производной:
У нас в любом случае будет производная произведения, тогда наша производная распадется на какое-то количество слагаемых либо просто синуса, либо просто косинуса и слагаемое с х умноженным на либо синус, либо косинус.
Заметим, что производная синуса равна
Тогда наше произведение в зависимости от n будет иметь разный вид.
Заметим, что всего различных слагаемых без множителя х будет n штук и все они будут иметь одинаковый знак
И по содержанию, и по знаку наши функции будут одинаковые. Осталось посчитать этот знак.
При n одинаковой четности знак один и тот же, в данной точке функция имеет вид
(производная меняет местами функции)
Мы можем записать для четных n знак у функции в виде где i - мнимая единица, для нечетных n знак тоже можно записать в виде ее степени
Для функции без множителя х формула такая (учитывая значения) - мы должны будем еще умножить на степень для нечетных и также умножить на n (n раз брали производную)
Для функции со множителем формула другая
Чтобы избавится от ненужных двоек в первом случае, умножим все на , и для того, чтобы все осталось как прежде во 2 случае, умножим только его часть на 2
Тогда общая формула производной имеет вид
Можем вынести множитель за скобки
4 Тогда запишем ряд Тейлора
Начинаю с 1 так как писалась формула производной от 1.
или проще
Пошаговое объяснение:
Вспомним формулу для разложения функции в ряд Тейлора
1 Запишем функцию
2 Найдем несколько производных:
...
3 Найдем общий вид производной:
У нас в любом случае будет производная произведения, тогда наша производная распадется на какое-то количество слагаемых либо просто синуса, либо просто косинуса и слагаемое с х умноженным на либо синус, либо косинус.
Заметим, что производная синуса равна
Тогда наше произведение в зависимости от n будет иметь разный вид.
Заметим, что всего различных слагаемых без множителя х будет n штук и все они будут иметь одинаковый знак
При n одинаковой четности знак один и тот же, в данной точке функция имеет вид
(производная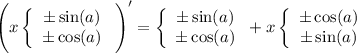 меняет местами функции)
меняет местами функции)
Мы можем записать для четных n знак у функции в виде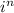 где i - мнимая единица, для нечетных n знак тоже можно записать в виде ее степени
где i - мнимая единица, для нечетных n знак тоже можно записать в виде ее степени 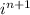
Для функции без множителя х формула такая (учитывая значения)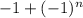 - мы должны будем еще умножить на степень для нечетных и также умножить на n (n раз брали производную)
- мы должны будем еще умножить на степень для нечетных и также умножить на n (n раз брали производную)
Для функции со множителем формула другая
Чтобы избавится от ненужных двоек в первом случае, умножим все на , и для того, чтобы все осталось как прежде во 2 случае, умножим только его часть на 2
, и для того, чтобы все осталось как прежде во 2 случае, умножим только его часть на 2
Тогда общая формула производной имеет вид
Можем вынести множитель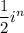 за скобки
за скобки
4 Тогда запишем ряд Тейлора
Начинаю с 1 так как писалась формула производной от 1.
f(2) = 2 * cos ( 2-2 ) = 2 * 1 = 2
Это и есть ответ