что бы решить данные примеры дроби нужно привести к общему знаменателю,т.е нужно найти такой знаменатель что бы его можно было разделить на знаменатели дробей без остатка и при этом что бы он делился на каждый из них:
/-дополнительные множетели(что бы их найти надо общий знаменатель поделить на знаменатель дроби
1) 2arcsin(-1)-4arcctg(-1) = -2π/2-4(π - arcctg1) = -π - 4(π - π/4) = -π - 4(3π/4) = -π - 3π = -4π.
2) ctgx>-1; πn < x < 3π/4 + πn, n∈Z.
3) 5cos^2x-6cosx=0; cosx(5cosx-6)=0;
cosx = 0 або 5cosx-6 = 0.
x = π/2 + πn, n∈Z. cosx = 1,2 - немає розв'язків.
Відповідь: π/2 + πn, n∈Z.
4) tg(arcsin1/2+arccos0) = -√3.
tg(arcsin1/2+arccos0) = tg(π/6+π/2) = -сtg(π/6) = -√3, що й треба було довести.
5) sinx+sin3x/cosx=0. ОДЗ: cosx ≠ 0.
sinx+sin3x = 0; 2sin2xcosx = 0;
sinx = 0 або cosx = 0 - не задовольняє ОДЗ.
x = πn, n∈Z.
6) tg(4x+π/4)+1 ≤ 0; tg(4x+π/4) ≤ -1; -π/2 + πn ≤ 4x+π/4 ≤ -π/4 + πn;
-π/2- π/4 + πn ≤ 4x ≤ -π/4 - π/4 + πn, n∈Z; -3π/4 + πn ≤ 4x ≤ -π/2 + πn, n∈Z;
-3π/8 + πn/4 ≤ x ≤ -π/8 + πn/4, n∈Z.
7) Розв'язати систему рівнянь: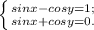
Додамо перше і друге рівняння системи: 
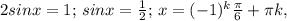k∈Z.
Віднімемо друге і перше рівняння системи:
Відповідь: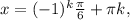
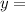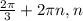k∈Z; 
±
∈Z.
что бы решить данные примеры дроби нужно привести к общему знаменателю,т.е нужно найти такой знаменатель что бы его можно было разделить на знаменатели дробей без остатка и при этом что бы он делился на каждый из них:
/-дополнительные множетели(что бы их найти надо общий знаменатель поделить на знаменатель дроби
8\15+6\7=(8\15)/7+(6\7)/15=56/105+90/105=146/105=1 41/105;
13\6+9\8=(13/6)/8+(9/8)/6=104/48+54/48=158/48=3 7/48;
11\2+5\8=(11/2)/4+(5/8)/1=44/8+5/8=49/8=1 1/8;
7\34+2\17=(7/34)/1+(2/17)/2=7/34+4/34=11/34;
5\3+8\9=(5/3)/3+(8/9)/1=15/9+8/9=23/9=2 5/9;
11\80+4\15=(11/80)/2+(4/15)/11=22/160+44/160=66/160=11/40;
3\7+21\4=(3/7)/4+(21/4)/7=12/28+147/28=159/28=5 19/28;
(ЕСЛИ ЧТО ТО НЕ ТАК ПИШИТЕ В КОММЕНТЫ)