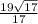здесь X,Y координаты вектора; xi, yi - координаты точки Аi; xj, yj - координаты точки Аj
Например, для вектора AB
X = x2 - x1; Y = y2 - y1
X = 1-2 = -1; Y = -2-1 = -3
AB(-1;-3)
AC(-3;-1)
BC(-2;2)
2) Модули векторов
Длина вектора a(X;Y) выражается через его координаты формулой:
3) Угол между прямыми
Угол между векторами a1(X1;Y1), a2(X2;Y2) можно найти по формуле:
где a1a2 = X1X2 + Y1Y2
Найдем угол между сторонами AB и AC
γ = arccos(0.6) = 53.130
4) Проекция вектора
Проекцию вектора b на вектор a можно найти по формуле:
Найдем проекцию вектора AB на вектор AC
5) Площадь треугольника
Пусть точки A1(x1; y1), A2(x2; y2), A3(x3; y3) - вершины треугольника, тогда его площадь выражается формулой:
В правой части стоит определитель второго порядка. Площадь треугольника всегда положительна.
Решение. Принимая A за первую вершину, находим:
По формуле получаем:
6) Деление отрезка в данном отношении
Радиус-вектор r точки A, делящий отрезок AB в отношении AA:AB = m1:m2, определяется формулой:
Координаты точки А находятся по формулам:
Уравнение медианы треугольника
Обозначим середину стороны BC буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.
M(0;-1)
Уравнение медианы AM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана AМ проходит через точки A(2;1) и М(0;-1), поэтому:
или
или
y = x -1 или y -x +1 = 0
7) Уравнение прямой
Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями:
Уравнение прямой AB
или
или
y = 3x -5 или y -3x +5 = 0
Уравнение прямой AC
или
или
y = 1/3x + 1/3 или 3y -x - 1 = 0
Уравнение прямой BC
или
или
y = -x -1 или y + x +1 = 0
8) Длина высоты треугольника, проведенной из вершины A
Расстояние d от точки M1(x1;y1) до прямой Ax + By + С = 0 равно абсолютному значению величины:
Найдем расстояние между точкой A(2;1) и прямой BC (y + x +1 = 0)
9) Уравнение высоты через вершину C
Прямая, проходящая через точку M0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:
Данное уравнение можно найти и другим Для этого найдем угловой коэффициент k1 прямой AB.
Уравнение AB: y = 3x -5, т.е. k1 = 3
Найдем угловой коэффициент k перпендикуляра из условия перпендикулярности двух прямых: k1*k = -1.
Подставляя вместо k1 угловой коэффициент данной прямой, получим :
3k = -1, откуда k = -1/3
Так как перпендикуляр проходит через точку C(-1,0) и имеет k = -1/3,то будем искать его уравнение в виде: y-y0 = k(x-x0).
Подставляя x0 = -1, k = -1/3, y0 = 0 получим:
y-0 = -1/3(x-(-1))
или
y = -1/3x - 1/3
Уравнение биссектрисы треугольника
Найдем биссектрису угла A. Точку пересечения биссектрисы со стороной BC обозначим М.
Уравнение высоты: , значит, уравнение противолежащей стороны будет выглядеть так: . Зная, что сторона проходит через точку (4; 6), найдём b: . То есть - уравнение одной из сторон.
Медиана пересекает сторону в точке (3; 2). Вычислим координаты второй вершины: .
Найдём третью вершину - точку пересечения медианы и высоты. Они пересекаются в точке (-2; 1).
Найдём уравнения остальных сторон по уравнению прямой :
1) Сторона, соединяющая точки (4; 6) и (-2; 1):
2) Сторона, соединяющая точки (2; -2) и (-2; 1):
Найдём точку пересечения высоты и противолежащей стороны (выразим их через y и приравняем):
Решение проводим с калькулятора.
Даны координаты треугольника: A(2,1), B(1,-2), C(-1,0).
1) Координаты векторов
Координаты векторов находим по формуле:
X = xj - xi; Y = yj - yi
здесь X,Y координаты вектора; xi, yi - координаты точки Аi; xj, yj - координаты точки Аj
Например, для вектора AB
X = x2 - x1; Y = y2 - y1
X = 1-2 = -1; Y = -2-1 = -3
AB(-1;-3)
AC(-3;-1)
BC(-2;2)
2) Модули векторов
Длина вектора a(X;Y) выражается через его координаты формулой:
3) Угол между прямыми
Угол между векторами a1(X1;Y1), a2(X2;Y2) можно найти по формуле:
где a1a2 = X1X2 + Y1Y2
Найдем угол между сторонами AB и AC
γ = arccos(0.6) = 53.130
4) Проекция вектора
Проекцию вектора b на вектор a можно найти по формуле:
Найдем проекцию вектора AB на вектор AC
5) Площадь треугольника
Пусть точки A1(x1; y1), A2(x2; y2), A3(x3; y3) - вершины треугольника, тогда его площадь выражается формулой:
В правой части стоит определитель второго порядка. Площадь треугольника всегда положительна.
Решение. Принимая A за первую вершину, находим:
По формуле получаем:
6) Деление отрезка в данном отношении
Радиус-вектор r точки A, делящий отрезок AB в отношении AA:AB = m1:m2, определяется формулой:
Координаты точки А находятся по формулам:
Уравнение медианы треугольника
Обозначим середину стороны BC буквой М. Тогда координаты точки M найдем по формулам деления отрезка пополам.
M(0;-1)
Уравнение медианы AM найдем, используя формулу для уравнения прямой, проходящей через две заданные точки. Медиана AМ проходит через точки A(2;1) и М(0;-1), поэтому:
или
или
y = x -1 или y -x +1 = 0
7) Уравнение прямой
Прямая, проходящая через точки A1(x1; y1) и A2(x2; y2), представляется уравнениями:
Уравнение прямой AB
или
или
y = 3x -5 или y -3x +5 = 0
Уравнение прямой AC
или
или
y = 1/3x + 1/3 или 3y -x - 1 = 0
Уравнение прямой BC
или
или
y = -x -1 или y + x +1 = 0
8) Длина высоты треугольника, проведенной из вершины A
Расстояние d от точки M1(x1;y1) до прямой Ax + By + С = 0 равно абсолютному значению величины:
Найдем расстояние между точкой A(2;1) и прямой BC (y + x +1 = 0)
9) Уравнение высоты через вершину C
Прямая, проходящая через точку M0(x0;y0) и перпендикулярная прямой Ax + By + C = 0 имеет направляющий вектор (A;B) и, значит, представляется уравнениями:
Данное уравнение можно найти и другим Для этого найдем угловой коэффициент k1 прямой AB.
Уравнение AB: y = 3x -5, т.е. k1 = 3
Найдем угловой коэффициент k перпендикуляра из условия перпендикулярности двух прямых: k1*k = -1.
Подставляя вместо k1 угловой коэффициент данной прямой, получим :
3k = -1, откуда k = -1/3
Так как перпендикуляр проходит через точку C(-1,0) и имеет k = -1/3,то будем искать его уравнение в виде: y-y0 = k(x-x0).
Подставляя x0 = -1, k = -1/3, y0 = 0 получим:
y-0 = -1/3(x-(-1))
или
y = -1/3x - 1/3
Уравнение биссектрисы треугольника
Найдем биссектрису угла A. Точку пересечения биссектрисы со стороной BC обозначим М.
Воспользуемся формулой:
Уравнение AB: y -3x +5 = 0, уравнение AC: 3y -x - 1 = 0
^A ≈ 530
Биссектриса делит угол пополам, следовательно угол NAK ≈ 26.50
Тангенс угла наклона AB равен 3 (т.к. y -3x +5 = 0). Угол наклона равен 72
^NKA≈ 1800 - 720 = 1080
^ANK ≈ 1800 - (1080 + 26.50) ≈ 45.50
tg(45.50) = 1
Биссектриса проходит через точку A(2,1), используя формулу, имеем:
y - y0 = k(x - x0)
y - 1 = 1(x - 2)
или
y = x -1
как я понял
Уравнение высоты: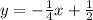 , значит, уравнение противолежащей стороны будет выглядеть так:
, значит, уравнение противолежащей стороны будет выглядеть так: 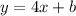 . Зная, что сторона проходит через точку (4; 6), найдём b:
. Зная, что сторона проходит через точку (4; 6), найдём b: 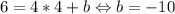 . То есть
. То есть 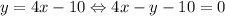 - уравнение одной из сторон.
- уравнение одной из сторон.
Медиана пересекает сторону в точке (3; 2). Вычислим координаты второй вершины: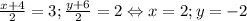 .
.
Найдём третью вершину - точку пересечения медианы и высоты. Они пересекаются в точке (-2; 1).
Найдём уравнения остальных сторон по уравнению прямой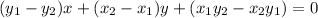 :
:
1) Сторона, соединяющая точки (4; 6) и (-2; 1):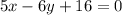
2) Сторона, соединяющая точки (2; -2) и (-2; 1):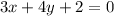
Найдём точку пересечения высоты и противолежащей стороны (выразим их через y и приравняем):
Длина высоты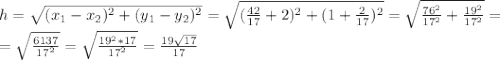
ответ: вершины: (4; 6), (2; -2), (-2; 1); уравнения сторон: ,
, 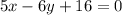 ,
, 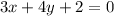 ; длина высоты:
; длина высоты: