Завод изготавливает изделия определенного типа. Вероятность наличия дефекта для каждого изделия равна Р1 = 0,95. Изделие осматривается одним контролером, он обнаруживает дефект с вероятностью Р2 = 0,97, а если дефект не обнаружен, то он отправляет его в готовую продукцию. Кроме того он может по ошибке забраковать изделие, не имеющее дефекта, вероятность этого Р3 = 0,05. Найти вероятность того, что изделие будет забраковано.

Показать ответ

Ответ:

nikomynenyzhen

09.09.2022 00:35

Найдите все значения а, при каждом из которых неравенство |x²-4x+a-5| ≤ 10 выполняется для всех x∈[a-5;a].

-10 ≤ x²-4x+a-5 ≤ 10

-x²+4x+5-10 ≤ a ≤ -x²+4x+5+1

-(x-2)²-1 ≤ a ≤ -(x-2)²+19 (1)

В декартовой системе координат а от х построим ГМТ удовлетворяющих неравенству (1). Эта область заключена между двумя параболами a = -(x-2)²-1 и a = -(x-2)²+19, включая сами параболы.

По условию a-5 ≤ x ≤ a, преобразуем:

$\displaystyle \left \{ {{a-5\le x} \atop {a\ge x}} \right. \quad \left \{ {{a\le x+5} \atop {a\ge x}} \right.\\\\ x\le a\le x+5\quad (2)$

Неравенство (2) задаёт область, которая ограничена двумя параллельными прямыми a=x-5 и a=x, включая границы.

Определим как взаимно расположены эти области.

$\displaystyle \left \{ {{a=x\qquad \qquad \quad } \atop {a=-x^2+4x-5}} \right. \quad \left \{ {{a=x\qquad \qquad \qquad } \atop {-x^2+4x-5-x=0}} \right. \\\\-\left( x-\dfrac32 \right) ^2-2\dfrac34 =0;\quad x\in \varnothing$

Прямая a=x не имеет общих точек с нижней границей графика (1), значит и прямая a=x+5 не имеет с ней общих точек.

$\displaystyle \left \{ {{a=x+5\qquad \qquad } \atop {a=-x^2+4x+15}} \right. \quad \left \{ {{x=a-5\qquad \qquad \qquad \qquad \quad } \atop {a+(a-5)^2-4(a-5)-15=0}} \right. \\\\a^2-13a+30=0;\quad D_1=169-120=7^2\\a=\dfrac{13\pm 7}2 =\{3;10\}$

Прямая a=x+5 пересекает верхнею границу графика (1) в двух различных точках с ординатами 3 и 10. Значит и прямая а=х пересекает эту границу, надём ординаты общих точек.

$\displaystyle \left \{ {{a=x\qquad \qquad \quad } \atop {a=-x^2+4x+15}} \right. \quad \left \{ {{a=x\qquad \qquad \qquad } \atop {a+a^2-4a-15=0}} \right. \\\\a^2-3a-15=0;\quad D_2=9+60=69\\a=\dfrac{3\pm \sqrt{69}}2$

При фиксированном a, все точки (x;a) графика (2) должны находится в области графика (1). По графику видно, что подходят только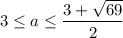 $3\le a\le \dfrac{3+\sqrt{69}}2$

ответ: $\bold a\in \left[ 3;\dfrac{3+\sqrt{69}}2 \right] .$

Разобраться с параметром ! найдите все значения а ,при каждом из которых неравенство /x^2-4x+a-5/<

0,0(0 оценок)

Ответ:

blackfantom

24.08.2022 08:22

1. Выполните действие:
а) 42-45=-3
г) 17-(-8)=17+8=25
б) -16-31 =-47
д) -3,7-2,6=-6.3
в) -15+18 =3
2. Найдите расстояние между точками координатной прямой:
а) М(-13) и К(-7) б) В(2,6) и Т(-1,2)
расстояние между точками то модуль
M-К=!-13!-!-7!=6 с одной стороны от 0 вычитание
В-T=!2.6!+!-1.2!=3.8 с разных сторон от0 сложение

3. Решите уравнение:
а) х – 2,8 = -1,6
x=-1.6+2.8
x=1.2
4. Цена товара повысилась с 84р. до 109,2р. На сколько процентов повысилась цена товара?
84руб-100
109.2руб-X
109.2*100:84=130.
130-100=30 на 30%-повысилась.
5. Решите уравнение |x-3|=6
x-3=6
x=9
x-3=-6
x=-3

0,0(0 оценок)

Популярные вопросы: Математика