Для лучшего понимания, построим известные функции.
Запишем формулу для вычисления площади:
По условию мы хотим чтобы данная площадь равнялась .
Сперва найдём интеграл:
Итого: .
Теперь решим уравнение относительно параметра а:
По условию задачи, поэтому второй корень отпадает, следовательно .
ответ: 8
Для лучшего понимания, построим известные функции.
Запишем формулу для вычисления площади:
По условию мы хотим чтобы данная площадь равнялась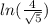 .
.
Сперва найдём интеграл:
Итого: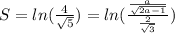 .
.
Теперь решим уравнение относительно параметра а:
По условию задачи,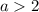 поэтому второй корень отпадает, следовательно
поэтому второй корень отпадает, следовательно 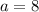 .
.
ответ: 8