Сначала найти производную функции у. Затем приравнять ее нулю. Получится квадратное уравнение. Его нужно решить, получить два корня. Тот, что меньший из корней, это максимум. Записать его в ответ. у'=2(х+9)(х+3)+ (x+9)^2=0 у'=0 2(х+9)(х+3)+ (x+9)^2=0 (x+9)(2х+6+х+9)=0(х+9)(3х+15)=0(х+9)(х+5)=0х=-9 и х=-5 точки экстремума при х ментьше -9 производная положительнаяфункция растётх больше -9 и меньше -5 падает функция(производная отрицательнапри х больше -5 растёттоесть х=-9 точка максимумаа х=-5 точка минимума(локального)у(-5)= (-5+9)^2(-5+3)+7 =(4)^2(-2)+7 =-32+7=-25
Боковые стороны трапеции равны по 8 см.
Пошаговое объяснение:
Трапеция называется равнобокой, если ее боковые стороны равны.
Пусть дана равнобокая трапеция ABCD. Ее боковые стороны равны AB = CD. Средняя линия EF = 5 см.
Средняя линия трапеции - это отрезок, соединяющий середины боковых сторон трапеции. Средняя линия трапеции равна полусумме оснований.
EF =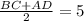 см
см
BC + AD = 2 * 5 = 10 (см)
Периметр равен сумме длин всех сторон, P = 26 см.
Сумма боковых сторон трапеции: AB + CD = P - (BC + AD) = 26 - 10 = 16 (см).
Боковые стороны: AB = CD =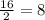 (см).
(см).
Затем приравнять ее нулю.
Получится квадратное уравнение.
Его нужно решить, получить два корня.
Тот, что меньший из корней, это максимум.
Записать его в ответ.
у'=2(х+9)(х+3)+ (x+9)^2=0
у'=0
2(х+9)(х+3)+ (x+9)^2=0 (x+9)(2х+6+х+9)=0(х+9)(3х+15)=0(х+9)(х+5)=0х=-9 и х=-5 точки экстремума
при х ментьше -9 производная положительнаяфункция растётх больше -9 и меньше -5 падает функция(производная отрицательнапри х больше -5 растёттоесть х=-9 точка максимумаа х=-5 точка минимума(локального)у(-5)= (-5+9)^2(-5+3)+7 =(4)^2(-2)+7 =-32+7=-25