1) пусть х - собственная скорость лыжника. Тогда х+2 - скорость лыжника на спуске, х-2 - скорость лыжника на подъеме. 2) уравнение: 8/(х-2) + 6/(х+2) = 1,5 8(х+2) + 6(х-2)= 1,5(х-2)(х+2) 8х+16+6х-12 = 1,5(х^2-4) 1,5х^2-6-14х-4=0 1,5х^2 -14х-10=0 Умножим обе части уравнения на 2: 3х^2-28х-20=0
х1= (28-32)(/2•3)=-4/6=-2/3 - не подходит, так как скорость не может быть <0.
х2=(28+32)/(2•3)= 60/6=10 км/ - собственная скорость лыжника.
2) на втором круге: 10 -20% = 10-10•0,2= 10-2=8 км/ч - собственная скорость лыжника на втором круге. 8+2=10 км/ч - скорость на спуске. 8-2=6 км/ч - скорость на подъеме. 8:6=4/3 часа уйдет на подъемы. 6:10=3/5 часа уйдет на спуски. 4/3 + 3/5= 20/15 + 9/15= 28/15 = 1 час 13/15 мин = 1 час 52 минуты потребуется на второй круг. 1,5 часа + 1 час 52 мин. = 1 ч 30 мин + 1 ч 52 мин. = 3 часа 22 минуты потребуется на всю дистанцию.
1. Площадь квадрата равна длине его стороны, возведённой в квадрат: , где - это сторона квадрата. Зная площадь, можем вычислить длину стороны: см. Периметр квадрата равен длине его стороны, умноженной на 4: см.
2. Периметр прямоугольника равен удвоенной сумме его смежных сторон. Пусть см - одна из сторон прямоугольника, а другая сторона на 3 см больше, то есть, см. Составляем уравнение:
Тогда другая сторона его см.
Площадь прямоугольника равна произведению длин его смежных сторон, тогда см².
3. Для начала найдём вторую сторону прямоугольника. Периметр прямоугольника равен удвоенной сумме его смежных сторон, тогда:
Тогда площадь прямоугольника см².
Прямоугольник имеет такую же площадь, что и квадрат. Площадь квадрата равна длине его стороны, возведённой в квадрат: , где - это сторона квадрата. Зная площадь, можем вычислить длину стороны: см. Периметр квадрата равен длине его стороны, умноженной на 4: см.
Тогда х+2 - скорость лыжника на спуске, х-2 - скорость лыжника на подъеме.
2) уравнение:
8/(х-2) + 6/(х+2) = 1,5
8(х+2) + 6(х-2)= 1,5(х-2)(х+2)
8х+16+6х-12 = 1,5(х^2-4)
1,5х^2-6-14х-4=0
1,5х^2 -14х-10=0
Умножим обе части уравнения на 2:
3х^2-28х-20=0
Дискриминант:
28^2 -4•3•(-20)= 784+ 240=1024
√1024=32
х1= (28-32)(/2•3)=-4/6=-2/3 - не подходит, так как скорость не может быть <0.
х2=(28+32)/(2•3)= 60/6=10 км/ - собственная скорость лыжника.
2) на втором круге:
10 -20% = 10-10•0,2= 10-2=8 км/ч - собственная скорость лыжника на втором круге.
8+2=10 км/ч - скорость на спуске.
8-2=6 км/ч - скорость на подъеме.
8:6=4/3 часа уйдет на подъемы.
6:10=3/5 часа уйдет на спуски.
4/3 + 3/5= 20/15 + 9/15= 28/15 = 1 час 13/15 мин = 1 час 52 минуты потребуется на второй круг.
1,5 часа + 1 час 52 мин. = 1 ч 30 мин + 1 ч 52 мин. = 3 часа 22 минуты потребуется на всю дистанцию.
1. Площадь квадрата равна длине его стороны, возведённой в квадрат: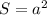 , где
, где  - это сторона квадрата. Зная площадь, можем вычислить длину стороны:
- это сторона квадрата. Зная площадь, можем вычислить длину стороны: 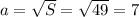 см. Периметр квадрата равен длине его стороны, умноженной на 4:
см. Периметр квадрата равен длине его стороны, умноженной на 4: 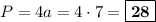 см.
см.
2. Периметр прямоугольника равен удвоенной сумме его смежных сторон. Пусть см - одна из сторон прямоугольника, а другая сторона на 3 см больше, то есть,
см - одна из сторон прямоугольника, а другая сторона на 3 см больше, то есть, 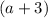 см. Составляем уравнение:
см. Составляем уравнение:
Тогда другая сторона его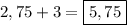 см.
см.
Площадь прямоугольника равна произведению длин его смежных сторон, тогда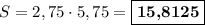 см².
см².
3. Для начала найдём вторую сторону прямоугольника. Периметр прямоугольника равен удвоенной сумме его смежных сторон, тогда:
Тогда площадь прямоугольника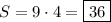 см².
см².
Прямоугольник имеет такую же площадь, что и квадрат. Площадь квадрата равна длине его стороны, возведённой в квадрат: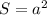 , где
, где  - это сторона квадрата. Зная площадь, можем вычислить длину стороны:
- это сторона квадрата. Зная площадь, можем вычислить длину стороны: 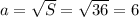 см. Периметр квадрата равен длине его стороны, умноженной на 4:
см. Периметр квадрата равен длине его стороны, умноженной на 4: 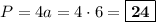 см.
см.