Возьмем производную данной функции, чтобы затем найти экстремум:
Известно, что производная принимает нулевое значение в точке экстремума ⇒ приравняв производную к нулю мы сможем его найти.
Рассмотрим знак производной до x = 0. При x = -1 производная отрицательна ⇒ функция убывает и при x = 0 минимум (можем так говорить, так как функция обычный куб). Затем производная становиться положительной и функция возрастает, пока x не становиться равен 4. Здесь достигается максимум. Потом производная становиться вновь отрицательной.
ответ: Максимум - (4;29), Минимум - (0;-3)
Пошаговое объяснение:
(Как я понимаю, ночью ставки выше)
Возьмем производную данной функции, чтобы затем найти экстремум:
Известно, что производная принимает нулевое значение в точке экстремума ⇒ приравняв производную к нулю мы сможем его найти.
Рассмотрим знак производной до x = 0. При x = -1 производная отрицательна ⇒ функция убывает и при x = 0 минимум (можем так говорить, так как функция обычный куб). Затем производная становиться положительной и функция возрастает, пока x не становиться равен 4. Здесь достигается максимум. Потом производная становиться вновь отрицательной.
Значит:
При x = 0 -
При x = 4 -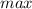
Подставим числа:
Пошаговое объяснение:
Лет-ние ра-дос-ти
Ког-да я вспо-ми-наю ле-то, то ду-маю толь-ко о хо-ро-шем
и ра-дост-ном.
В этом го-ду я в пер-вый раз по-ехал в ла-герь. Сна-ча-ла
мне там не очень пон-ра-ви-лось, я очень ску-чал по до-му.
Но -я за-пи-сал-ся в авиа-мо-дель-ный кру-жок и пе-ре-стал
ску-чать. Там я по-дру-жил-ся со мно-ги--ми ре-бя-та-ми. Но
са-мое глав-ное — я сде-лал на-стоя-щую мо-дель са-мо-ле-та! Мы
за-пус-ка-ли свои мо-де-ли с вы-со-кой го-ры, и они пре-крас-но
ле-та-ли. Еще мне за-пом-ни-лись спор-тив-ные со-рев-но-ва-ния —
эс-та-фе-та и во-лей-бол. Наш от-ряд за-нял пер-вое мес-то по
во-лей-бо-лу, и все очень ра-до-ва-лись. Очень хо-чет-ся по-ехать
в ла-герь сле-дую-щим ле-том, встре-тить-ся там с друзь-ями.
Списать текст, делить на слоги для переноса, поставить
ударение, подчеркнуть мягкие согласные.