Перепишем уравнение в виде y'=(3*y-4*x)/(2*y-3*x). Разделив числитель и знаменатель правой части на x и полагая z=y/x, приходим к уравнению y'=(3*z-4)/(2*z-3). А так как y=z*x, то y'=z'*x+z, и данное уравнение принимает вид z'*x+z=(3*z-4)/(2*z-3), или z'*x=-2*(z²-3*z+2)/(2*z-3). И так как z'=dz/dx, а 2*z-3=(z²-3*z+2)', то окончательно это уравнение можно записать в виде d(z²-3*z+2)/(z²-3*z+2)=-2*dx/x. Интегрируя обе части, получаем ln/z²-3*z+2/=-2*ln/x/+ln/C/, где C - произвольная, но не равная нулю постоянная. Отсюда z²-3*z+2=C/x², или y²/x²-3*y/x+2-C/x²=(y²-C)/x²-3*y/x+2=0.
ответ: (y²-C)/x²-3*y/x+2=0.
Пошаговое объяснение:
Перепишем уравнение в виде y'=(3*y-4*x)/(2*y-3*x). Разделив числитель и знаменатель правой части на x и полагая z=y/x, приходим к уравнению y'=(3*z-4)/(2*z-3). А так как y=z*x, то y'=z'*x+z, и данное уравнение принимает вид z'*x+z=(3*z-4)/(2*z-3), или z'*x=-2*(z²-3*z+2)/(2*z-3). И так как z'=dz/dx, а 2*z-3=(z²-3*z+2)', то окончательно это уравнение можно записать в виде d(z²-3*z+2)/(z²-3*z+2)=-2*dx/x. Интегрируя обе части, получаем ln/z²-3*z+2/=-2*ln/x/+ln/C/, где C - произвольная, но не равная нулю постоянная. Отсюда z²-3*z+2=C/x², или y²/x²-3*y/x+2-C/x²=(y²-C)/x²-3*y/x+2=0.
Если все числа правильно записаны, то ответ получается вот такой ( смотри ниже. Но смущают не целые числа, хотя всё остальное правильно)
Пошаговое объяснение:
Пусть во 2 день продали на х сум, тогда по условию в 1 день ( х + 23500) сум, а в 3 день ( х + 23500 - 56000) = ( х - 32500). Всего продано на
1 971 500 сум. Составим и решим уравнение:
( х + 23500) + х + ( х - 32500) = 1 971 500
3х - 9000 = 1 971 500
3х = 1 971 500 + 9000
3х = 1 980 500
х= 1 980 500 : 3
х = 660 166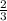
Значит, во второй день было продано на 660 166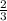
сум, тогда в первый день на 683 666
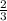сум, а в трети1 день 627 666
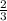сум.