Формула Р=2•(а+в); или Р=2а+2в; тут Р=20см; Ширина=а; длина=в=(а+2см); подставляем периметр=2•ширину+2•длину; =>> 20=2а+2•(а+2); 20=2а+2а+4; =>> 20-4=4а; 16=4а; а=16:4; а=4См; Ширина=4см длина=а+2=4+2=6см; проверка 4•2+6•2=8+12=20см. можно ещё так; Р=20; значит половина 20:2=10см это Ширина+длина; длина на 2см больше, значит 10-2=8см, остальное делим на 2, потому что теперь стороны одинаковы; 8:2=4см Ширина; теперь добавляем назад 2см что вычли 4+2=6см длина; проверяем 6+4=10см половина периметра; 10•2=20см весь периметр; или 4•2+6•2=8+12=20см; ответ: длина 6см.
Отрезать части по 15 см 2 раза, а по 12 см - 6 раз.
Отрезать части по 15 см 6 раз, а по 12 см - 1 раз.
Решение:Пусть у нас будет
кусков проволоки по 15 см, и 
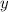- по 12 см. При этом 
и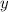 
- натуральные (и не 0, так как 102 не делится ни на 12, ни на 15).
Имеем линейное Диафантово уравнение в целых числах: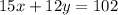
. И будем просто перебирать 
от 1 до 6, и смотреть, есть ли для него натуральный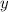 
в каждом случае.
Пусть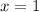
, тогда 
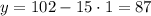, на 12 не делится.
Пусть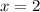
, тогда 
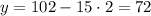, 72:12=6.
Пусть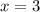
, тогда 
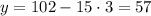, на 12 не делится.
Пусть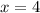
, тогда 
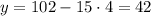, на 12 не делится.
Пусть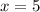
, тогда 
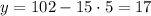, на 12 не делится.
Пусть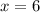
, тогда 
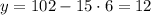, 12:12=1.
Итого имеем целых два