ответ:
Пошаговое объяснение:
Пусть:
Тогда уравнение принимает вид:
Заметим, что если корень уравнения , то он и корень уравнения:
, действительно:
Найдем все такие корни:
Заметим, что функция - монотонно возрастает.
Предположим, что в уравнении существует корень , такой, что
Рассмотрим случай: .
Поскольку, - монотонно возрастает, то если для некоторых двух ее аргументов выполнено неравенство: , то верно и данное неравенство:
Из данного утверждения следует, что :
Но , то есть мы пришли к противоречию.
Аналогично показывается невозможность утверждения для случая
. Таким образом, других корней помимо нет.
ответ:
Пошаговое объяснение:
Пусть:
Тогда уравнение принимает вид:
Заметим, что если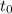 корень уравнения
корень уравнения 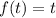 , то он и корень уравнения:
, то он и корень уравнения:
Найдем все такие корни:
Заметим, что функция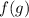 - монотонно возрастает.
- монотонно возрастает.
Предположим, что в уравнении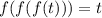 существует корень
существует корень 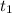 , такой, что
, такой, что 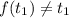
Рассмотрим случай: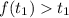 .
.
Поскольку,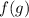 - монотонно возрастает, то если для некоторых двух ее аргументов выполнено неравенство:
- монотонно возрастает, то если для некоторых двух ее аргументов выполнено неравенство:  , то верно и данное неравенство:
, то верно и данное неравенство: 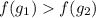
Из данного утверждения следует, что :
Но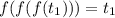 , то есть мы пришли к противоречию.
, то есть мы пришли к противоречию.
Аналогично показывается невозможность утверждения для случая