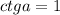Я подумал и решил написать - Чем полезны комнатные растения.Комнатные растения - они очень нужны человеку в доме. Они поглощают углекислый газ, а взамен выделяют кислород. Комнатные растения очищают воздух от собравшиеся пыли и бактерий. Из некоторых комнатных растений можно делать лекарства, которые лечат человека. Растение может защитить человека от простуды и от некоторых болезней, которые очень часто распространяются. Есть еще растения для удачи и счастья. Они приносят удачу и счастье в дом. Вот этим и полезны комнатные растения!
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Для того, чтобы найти синус по известному косинусу,
Тангенс по известному косинусу
Котангенс по известному синусу или наоборот
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: ×
Я подумал и решил написать - Чем полезны комнатные растения.Комнатные растения - они очень нужны человеку в доме. Они поглощают углекислый газ, а взамен выделяют кислород. Комнатные растения очищают воздух от собравшиеся пыли и бактерий. Из некоторых комнатных растений можно делать лекарства, которые лечат человека. Растение может защитить человека от простуды и от некоторых болезней, которые очень часто распространяются. Есть еще растения для удачи и счастья. Они приносят удачу и счастье в дом. Вот этим и полезны комнатные растения!
ДА
Пошаговое объяснение:
Приближенное число для каждой из известных функций можно найти по определению. Для одних можно указать точные значения, для других – только приблизительные.
Линии тригонометрических функций – это линии, которые изображаются вместе с единичной окружностью. Они имеют точку отсчета и единичный отрезок, которая равна единице в координатной системе. Они используются для наглядного изображения значений.
Для того, чтобы найти синус по известному косинусу,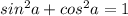
Тангенс по известному косинусу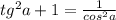
Котангенс по известному синусу или наоборот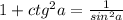
Тангенс через котангенс или наоборот можно найти благодаря удобной формуле: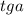 ×
×