ответ: невозможно
Пошаговое объяснение:
1 вариант: по т. Косинусов: c² = a² + b² - 2ab*cos(a,b)
c - гипотенуза (очевидно, самый большой отрезок у нас 3)
a, b - катеты (1 и 2)
Подставляем в формулу: 9 = 1 + 4 - 2*2*сos(a,b)
9 = 5 - 4cos(a,b)
4 = -4cos(a,b)
cos = -1, => угол между катетами равен 180 (т.е а и b - одна прямая) - поэтому треугольник невозможен
2 вариант: известно, что сумма двух сторон в треугольнике всегда меньше третьей (теорема о соотношении сторон треугольника), т.е a + b < c
В данном случае 2+1 < 3 не выполняется, => треугольник невозможен
Для начала вспомним все необходимые формулы. В нашем случае это формула нахождения площади и периметра прямоугольника.
, где - площадь, - длина, - ширина.
, где - периметр, - длина, - ширина.
Известно, что м², а м. Следовательно, можем вычислить ширину первого водоема.
м
Также известно, что м, а м. Следовательно, можем вычислить ширину второго водоема.
Так как в задании требуется сравнить площади водоемов, нужно найти .
м²
В задании требуется сравнить ширину первого и второго водоема и их площади.
1) м, м
2) м², м²
ответ: невозможно
Пошаговое объяснение:
1 вариант: по т. Косинусов: c² = a² + b² - 2ab*cos(a,b)
c - гипотенуза (очевидно, самый большой отрезок у нас 3)
a, b - катеты (1 и 2)
Подставляем в формулу: 9 = 1 + 4 - 2*2*сos(a,b)
9 = 5 - 4cos(a,b)
4 = -4cos(a,b)
cos = -1, => угол между катетами равен 180 (т.е а и b - одна прямая) - поэтому треугольник невозможен
2 вариант: известно, что сумма двух сторон в треугольнике всегда меньше третьей (теорема о соотношении сторон треугольника), т.е a + b < c
В данном случае 2+1 < 3 не выполняется, => треугольник невозможен
Для начала вспомним все необходимые формулы. В нашем случае это формула нахождения площади и периметра прямоугольника.
Известно, что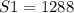 м², а
м², а 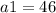 м. Следовательно, можем вычислить ширину первого водоема.
м. Следовательно, можем вычислить ширину первого водоема.
Также известно, что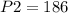 м, а
м, а 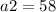 м. Следовательно, можем вычислить ширину второго водоема.
м. Следовательно, можем вычислить ширину второго водоема.
Так как в задании требуется сравнить площади водоемов, нужно найти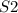 .
.
В задании требуется сравнить ширину первого и второго водоема и их площади.
1)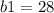 м,
м, 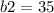 м
м
2)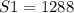 м²,
м², 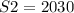 м²
м²