602,88
-6,3
2,25
( -∞; 1,1 )
10
Нужен рисунок трапеции
2, 3
34,2
0,1
Пошаговое объяснение:
4,8 · 0,6 + 6 · 10² = 2,88+600 = 602,88
9(х + 7) = -х
9x+63 = -x
10x = -63
x = -6,3
3х² - х + 2 при х = 0,5
3(0,5)²-0,5+2 = 3*0,25+1,5 = 0,75+1,5 = 2,25
2(4х – 7) < -3 – 2х
8x-14 < -3-2x
10x < 11
x < 1,1
ответ: ( -∞; 1,1 )
По теореме Пифагора
x² = 6² + 8²
x² = 36+64
x² = 100
x = ± 10
ответ: 10
Без рисунка посчитать нельзя
Верные - 2, 3
30000/100=х/14
х=30000*0,14
х=4200 руб - доход
30000+4200=34200 рублей
34200 рублей = 34,2 тыс рублей
1/10 = 0,1
1)
Проверим точку . Равенство не выполняется.
Значит, домножим и поделим на .
Получим .
Имеем .
Выражение в числителе над эквивалентно , т.к. имеет те же корни .
Значит, единственный корень: .
2)
При данных ограничениях решить уравнение невозможно. Сумма слева может расходиться (т.е равняться ), ведь знаменатель прогрессии .
Пусть
Слева имеем сумму бесконечно убывающей геометрической прогрессии. Значит выражение можно свернуть в:
Или .
По условию подходит один корень:
3)
Для простоты преобразуем к виду:
.
Слева сумма бесконечно убывающей геометрической прогрессии.
И корни:
602,88
-6,3
2,25
( -∞; 1,1 )
10
Нужен рисунок трапеции
2, 3
34,2
0,1
Пошаговое объяснение:
4,8 · 0,6 + 6 · 10² = 2,88+600 = 602,88
9(х + 7) = -х
9x+63 = -x
10x = -63
x = -6,3
3х² - х + 2 при х = 0,5
3(0,5)²-0,5+2 = 3*0,25+1,5 = 0,75+1,5 = 2,25
2(4х – 7) < -3 – 2х
8x-14 < -3-2x
10x < 11
x < 1,1
ответ: ( -∞; 1,1 )
По теореме Пифагора
x² = 6² + 8²
x² = 36+64
x² = 100
x = ± 10
ответ: 10
Без рисунка посчитать нельзя
Верные - 2, 3
30000/100=х/14
х=30000*0,14
х=4200 руб - доход
30000+4200=34200 рублей
34200 рублей = 34,2 тыс рублей
1/10 = 0,1
1)
Проверим точку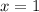
. Равенство не выполняется.
Значит, домножим и поделим на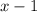
.
Получим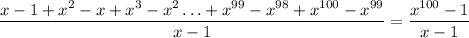
.
Имеем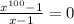
.
Выражение в числителе над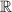
эквивалентно 
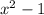, т.к. имеет те же корни ![x^{100} = 1 \Rightarrow x = \sqrt[100]{1} = \pm 1](/tpl/images/0977/3396/ad536.png)
.
Значит, единственный корень: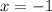
.
2)
При данных ограничениях решить уравнение невозможно. Сумма слева может расходиться (т.е равняться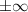
), ведь знаменатель прогрессии 
.
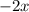Пусть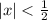
Слева имеем сумму бесконечно убывающей геометрической прогрессии. Значит выражение можно свернуть в:
Или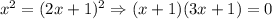
.
По условию подходит один корень: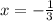
3)
Для простоты преобразуем к виду:
Слева сумма бесконечно убывающей геометрической прогрессии.
И корни: