Заметим , что среди трех последовательных чисел всегда есть число кратное 3. А так же одно или два числа кратных 2. (Из соображения того, что есть всего 3 остатка от деления на 3 : 0;1;2, а при делении на 2 : 0;1).
Вытяним все степени двойки из произведения трех последовательных чисел , тогда получим:
an1, bn2, cn3 - простые множители большие двух ,каждого из трех последовательных натуральных чисел.( простые числа)
Покажем ,что три последовательных числа не имеют общих простых делителей больше 2. Предположим , что n делится на p : n=k*p , тогда n+2=k*p+2, тк p>2 , то 2 не делится на p , а значит n+2 не делится на p. Аналогично n+1 не делится на p : n+1=k*p+1 тк 1 не делится на p. Так же доказывается для случая делимости на простое чисел n+1 и n+2.
А значит невозможны равенства:
ak1=bk2 , ak1=ck2 , bk1=ck1.
То есть в трех сомножителях нет одинаковых простых множителей .
Предположим что: n*(n+1)*(n+2) является cтепенью q натурального числа N.
N=p1^i1 *p2^i2 *p3^i3...*pm^Im
pm-простые числа.
N^q=p1^qi1 *p2^qi2 *p3^qi3...*pm^qIm.
Поскольку до этого было доказано , что невозможны равенства:
Возьмём для простоты вычислений числа n-1, n, n+1. Пусть произведение этих чисел — это k-тая степень какого-то числа: . Зная, что два последовательных натуральных числа всегда взаимно простые, получаем, что число n взаимно простое с числами n-1, n+1, то есть n не имеет общих множителей в разложении с числами n-1 и n+1. Значит, каждый множитель n находится в k-той степени — само число n — это k-тая степень. Но тогда и (n-1)(n+1) = n²-1 является k-той степенью. Если возвести число n в квадрат, оно всё равно останется числом в степени k: . Но тогда n²-1 и n² — это два последовательных числа, являющиеся k-той степенью. Если взглянуть на графики степенных функций, становится ясно, что такого быть не может. Значит, и произведение трех последовательных натуральных чисел не является степенью натурального числа.
Заметим , что среди трех последовательных чисел всегда есть число кратное 3. А так же одно или два числа кратных 2. (Из соображения того, что есть всего 3 остатка от деления на 3 : 0;1;2, а при делении на 2 : 0;1).
Вытяним все степени двойки из произведения трех последовательных чисел , тогда получим:
n*(n+1)*(n+2)=2^r *(a1^f1*a2^f2*a3^f3...*an1^fn) *(b1^g1* b2^g2*b3^g3*..bn2^gn)*(c1^h1* c2^h2 *c3*h3..cn3^hn)
an1, bn2, cn3 - простые множители большие двух ,каждого из трех последовательных натуральных чисел.( простые числа)
Покажем ,что три последовательных числа не имеют общих простых делителей больше 2. Предположим , что n делится на p : n=k*p , тогда n+2=k*p+2, тк p>2 , то 2 не делится на p , а значит n+2 не делится на p. Аналогично n+1 не делится на p : n+1=k*p+1 тк 1 не делится на p. Так же доказывается для случая делимости на простое чисел n+1 и n+2.
А значит невозможны равенства:
ak1=bk2 , ak1=ck2 , bk1=ck1.
То есть в трех сомножителях нет одинаковых простых множителей .
Предположим что: n*(n+1)*(n+2) является cтепенью q натурального числа N.
N=p1^i1 *p2^i2 *p3^i3...*pm^Im
pm-простые числа.
N^q=p1^qi1 *p2^qi2 *p3^qi3...*pm^qIm.
Поскольку до этого было доказано , что невозможны равенства:
ak1=bk2 , ak1=ck2 , bk1=ck1.
То справедливо, что:
n*(n+1)*(n+2)=2^qr *(a1^qf1*a2^qf2*a3^qf3...*an1^qfn) *(b1^qg1* b2^qg2*b3^qg3*..bn2^qgn)*(c1^qh1* c2^qh2 *c3^qh3..cn3^qhn)
Откуда очевидно , что для соседних четного и нечетного числа верно что: n=x^q , n+1=y^q.
То есть верно что:
x^q-y^q=1 , что не является возможным для натуральных чисел x,y,q.
Поскольку x^q-y^q делится на x-y по формуле разности степеней. x-y=1
Но тогда x^n-y^n>1 , то есть мы пришли к противоречию.
Вывод: произведение трех последовательных чисел не является степенью целого числа.
Возьмём для простоты вычислений числа n-1, n, n+1. Пусть произведение этих чисел — это k-тая степень какого-то числа: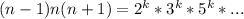
. Зная, что два последовательных натуральных числа всегда взаимно простые, получаем, что число n взаимно простое с числами n-1, n+1, то есть n не имеет общих множителей в разложении с числами n-1 и n+1. Значит, каждый множитель n находится в k-той степени — само число n — это k-тая степень. Но тогда и (n-1)(n+1) = n²-1 является k-той степенью. Если возвести число n в квадрат, оно всё равно останется числом в степени k: 
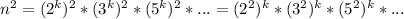. Но тогда n²-1 и n² — это два последовательных числа, являющиеся k-той степенью. Если взглянуть на графики степенных функций, становится ясно, что такого быть не может. Значит, и произведение трех последовательных натуральных чисел не является степенью натурального числа.