Знайти найбільше і найменше значення функції f(x) = x³ - 3x² + 3 на проміжку = [-2;2]

на промежутке  [-2;2]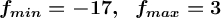    

Пошаговое объяснение:

Первая производная

f'(x) = (x³ - 3x² + 3) = 3x² -6x = 3x( x - 2)

Найдем критические точки

3х(х - 2 ) = 0

x1 = 0;   x2 = 2   - критические точки.

Найдем значение функции в критических точках и на концах интервала

f(0) = 3

f(2) = -1

f(-2) = -17

Таким образом,

максимум функции достигается в критической точке x1 = 0   f(0) = 3;

минимум функции достигается на конце интервала х3 = -2    f(-2) = -17