Во-первых, умные далеко не все, просто именно те, кто умён учат других. Во-вторых, умными они становятся постепенно, учась на своих же ошибках (см. ниже).
И ещё добавлю, насчёт твоего "предела" - это fixed mindset (фиксированное мышление), не очень прогрессивное мышление. По моему мнению, лучше - growth mindser (установка на рост). Почитай про них на досуге.
Почему когда реально стараешься, а выходит из этого "ничего"
Ну, как минимум, это нормально. Большинство открытий совершаются путём бесчисленных проб и ошибок. Ошибаться, терпеть неудачи - нормально, с этим, увы, ничего не поделать. Но знаешь, с ошибок можно неплохо разобраться в вопросе - учиться и улучшать себя.
P.S. , по сути, ничего не значат, ибо это лишь число в базе данных, не забивай ими свою голову.
Вообще говоря, эту задачу можно решать с метода множителей Лагранжа, но я постараюсь обойтись без них. Задача максимизировать произведение abc трех положительных чисел при условии постоянства суммы a²+b²+c² их квадратов. Понятно. что вместо произведения чисел можно рассмотреть произведение их квадратов, а обозначив их буквами x, y, z соответственно, получаем более симпатичную формулировку: максимизировать произведение xyz положительных чисел при условии x+y+z=K (K - некоторое положительное число).
Как всегда в таких задачах, ищем точки, в которых обе частные производные равны нулю (иными словами, точки, в которых первый дифференциал равен нулю):
Сокращение на x и y оправдано их положительностью. (Кстати, если даже попробовать представить себе параллелепипед с нулевой стороной, шансов у такого вырожденца иметь наибольший объем нет никаких.) Далее теория советует исследовать второй дифференциал в найденных критических точках на положительную или отрицательную определенность с критерия Сильвестра. Давайте последуем этим советам.
Видим, что угловой минор первого порядка -2K/3<0; угловой минор второго порядка K²/3>0. Значит, второй дифференциал отрицательно определен, а это в условиях равенства нулю дифференциала первого порядка означает наличие точки максимума.
Итак, доказано, что наибольший объем среди параллелепипедов с фиксированной диагональю имеет куб.
Подскажите, почему все такие умные?
Во-первых, умные далеко не все, просто именно те, кто умён учат других. Во-вторых, умными они становятся постепенно, учась на своих же ошибках (см. ниже).
И ещё добавлю, насчёт твоего "предела" - это fixed mindset (фиксированное мышление), не очень прогрессивное мышление. По моему мнению, лучше - growth mindser (установка на рост). Почитай про них на досуге.
Почему когда реально стараешься, а выходит из этого "ничего"
Ну, как минимум, это нормально. Большинство открытий совершаются путём бесчисленных проб и ошибок. Ошибаться, терпеть неудачи - нормально, с этим, увы, ничего не поделать. Но знаешь, с ошибок можно неплохо разобраться в вопросе - учиться и улучшать себя.
P.S. , по сути, ничего не значат, ибо это лишь число в базе данных, не забивай ими свою голову.
Вообще говоря, эту задачу можно решать с метода множителей Лагранжа, но я постараюсь обойтись без них. Задача максимизировать произведение abc трех положительных чисел при условии постоянства суммы a²+b²+c² их квадратов. Понятно. что вместо произведения чисел можно рассмотреть произведение их квадратов, а обозначив их буквами x, y, z соответственно, получаем более симпатичную формулировку: максимизировать произведение xyz положительных чисел при условии x+y+z=K (K - некоторое положительное число).
Как всегда в таких задачах, ищем точки, в которых обе частные производные равны нулю (иными словами, точки, в которых первый дифференциал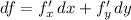
равен нулю):
Видим, что угловой минор первого порядка -2K/3<0; угловой минор второго порядка K²/3>0. Значит, второй дифференциал отрицательно определен, а это в условиях равенства нулю дифференциала первого порядка означает наличие точки максимума.
Итак, доказано, что наибольший объем среди параллелепипедов с фиксированной диагональю имеет куб.