Застосуємо формулу Ліувілля-Остроградського.
де — постійна константа.
За означення визначника, отримаємо
Застосуємо формулу Ліувілля-Остроградського.
де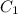 — постійна константа.
— постійна константа.
За означення визначника, отримаємо