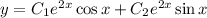Рівняння вигляду де — задані числа, є лінійним однорідним диференціальним рівнянням (ЛОДР) другого порядку зі сталими коефіцієнтами.
Метод Ейлера (метод характеристичних рівнянь) дозволяє знаходити загальний розв'язок для вказаного рівняння.
Розв'язок цього рівняння шукаємо у вигляді де — деяка стала (дійсна чи комплексна). Тоді, якщо то
— характеристичне рівняння
Можливі три випадки:
➀ і — дійсні,
Фундаментальна система розв'язків: — функції лінійно незалежні, бо
Загальний розв'язок:
Приклад: а)
Метод Ейлера:
Характеристичне рівняння:
Відповідь:
Приклад: в)
➁ і — дійсні,
Якщо покласти , то ці функції лінійно залежні, бо
➂ і — комплексно спряжені,
Приклад: б)
Отже,
Рівняння вигляду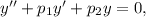 де
де 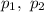 — задані числа, є лінійним однорідним диференціальним рівнянням (ЛОДР) другого порядку зі сталими коефіцієнтами.
— задані числа, є лінійним однорідним диференціальним рівнянням (ЛОДР) другого порядку зі сталими коефіцієнтами.
Метод Ейлера (метод характеристичних рівнянь) дозволяє знаходити загальний розв'язок для вказаного рівняння.
Розв'язок цього рівняння шукаємо у вигляді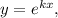 де
де 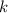 — деяка стала (дійсна чи комплексна). Тоді, якщо
— деяка стала (дійсна чи комплексна). Тоді, якщо 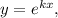 то
то 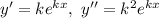
Можливі три випадки:
➀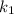 і
і 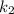 — дійсні,
— дійсні, 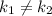
Фундаментальна система розв'язків: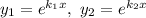 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 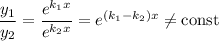
Загальний розв'язок: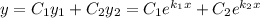
Приклад: а)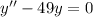
Метод Ейлера: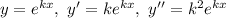
Характеристичне рівняння: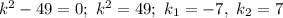
Загальний розв'язок: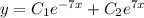
Відповідь: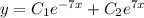
Приклад: в)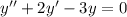
Метод Ейлера: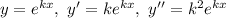
Характеристичне рівняння: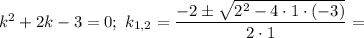
Загальний розв'язок: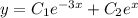
Відповідь: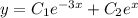
➁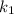 і
і 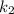 — дійсні,
— дійсні, 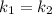
Якщо покласти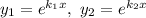 , то ці функції лінійно залежні, бо
, то ці функції лінійно залежні, бо 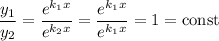
Фундаментальна система розв'язків: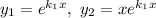 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 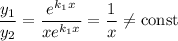
Загальний розв'язок: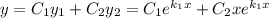
➂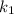 і
і 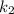 — комплексно спряжені,
— комплексно спряжені, 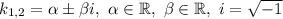
Фундаментальна система розв'язків: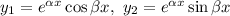 — функції лінійно незалежні, бо
— функції лінійно незалежні, бо 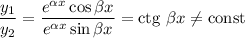
Загальний розв'язок: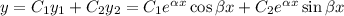
Приклад: б)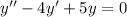
Метод Ейлера: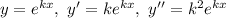
Характеристичне рівняння: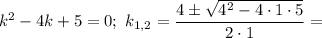
Отже,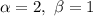
Загальний розв'язок: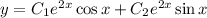
Відповідь: