k = 3
Объяснение:
Угловой коэффициент касательной k к графику функции f(x) в точке х0 есть значение производной f ' (x) в точке х0.
То есть, нам нужно найти производную f(x) и просто подставить в неё х0.
f(x) = 19sinx + 3x
f '(x) = 19cosx + 3
k = f '(x0) = f '(-/2) = 19cos(-/2) + 3 = 19•0 + 3 = 0 + 3 = 3
*Если я верно понял, в задании могла быть опечатка и подразумевалось не (-2), а именно (-/2)
k = 3
Объяснение:
Угловой коэффициент касательной k к графику функции f(x) в точке х0 есть значение производной f ' (x) в точке х0.
То есть, нам нужно найти производную f(x) и просто подставить в неё х0.
f(x) = 19sinx + 3x
f '(x) = 19cosx + 3
k = f '(x0) = f '(-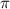 /2) = 19cos(-
/2) = 19cos(-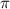 /2) + 3 = 19•0 + 3 = 0 + 3 = 3
/2) + 3 = 19•0 + 3 = 0 + 3 = 3
k = 3
*Если я верно понял, в задании могла быть опечатка и подразумевалось не (-2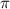 ), а именно (-
), а именно (-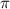 /2)
/2)