Простое число р при р>3 имеет вид р=6k+1 или p=6l-1, где k, l - некоторые натуральные числа
Поэтому либо делится на 12, так как множитель 12 делится на 12, а один из множителей k или 3k+1 делится на 2(если k четное, значит k - делится на 2, если k - нечетное, то 3k+1- четное и делится на 2)
либо
делится на 12, так как множитель 12 делится на 12, а один из множителей l или 3l-1 делится на 2(если l четное, значит l - делится на 2, если l - нечетное, то 3l-1- четное и делится на 2)
В обоих возможных случаях делится на 12*2=24. Доказано
Тебе нужны области больше нуля, а значит те, где плюс. Поэтому ответ от минус бесконечности до -3 и от 7 до плюс бесконечности (точки -3 и 7 незакрашенные, т.к. неравенство нестрогое (т.е. знак >, а не >=) )
ответ: (-бесконечности; -3) и (7; + бесконечности).
Простое число р при р>3 имеет вид р=6k+1 или p=6l-1, где k, l - некоторые натуральные числа
Поэтому либо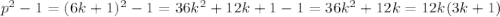
делится на 12, так как множитель 12 делится на 12, а один из множителей k или 3k+1 делится на 2(если k четное, значит k - делится на 2, если k - нечетное, то 3k+1- четное и делится на 2)
либо
В обоих возможных случаях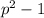
делится на 12*2=24. Доказано
x² - 4x - 21 > 0
x²-4x-21=0
D=b²-4ac=100
x₁=(4+10)/2=7
x₂=(4-10)/2=-3
(x-7)(x+3)>0
+ - +
___-37___
Подставим любое число из области x>7, например 10
100-40-21>0
39>0 - верно, значит здесь будет +
Теперь из промежутка -3<x<7, например 0
0-0-21>0
-21>0 = неверно, значит здесь знак -
И наконец из промежутка x<-3, например -10
100+40-21>0
119>0 - верно, значит здесь +
Тебе нужны области больше нуля, а значит те, где плюс. Поэтому ответ от минус бесконечности до -3 и от 7 до плюс бесконечности (точки -3 и 7 незакрашенные, т.к. неравенство нестрогое (т.е. знак >, а не >=) )
ответ: (-бесконечности; -3) и (7; + бесконечности).