Посмотрим на клетку, находящуюся в левом верхнем углу, по условию задачи, в этой клетке не 5,4,3, но это не 1 т.к. оно больше какого-то числа. Следовательно там 2. Тогда в клетке, что ниже 1.
Посмотрим на самую нижнюю клетку этого столбца - она может быть или 3 или 5. Посмотрим всю строчку. В строке есть 3, значит в этой клетке 5.
В итоге первый столбец : 2 1 4 3 5, а верхняя строка 2 3 5 1 4.
Теперь заполним 2 столбец.
В нём два знака > и туда подойдут 4 и 5(не 3 т.к. она наверху) Рядом с 4 не может быть 4, поэтому ставим 5, а две клетки ниже 4. Остаётся 2 и 1. Посмотрим на соседний столбец и в итоге получаем : 3 4 5 1 2(4 и 2 не работает)
Заполним предпоследнюю строку(там есть знак). В и клеточке, слева от которой стоит знак будет 5, так как 2 больше только 1, а 1 стоит выше, а 3 и 4 в этом столбике есть. Оставим пока так и перейдем к тем строчкам, которые мы можем теперь заполнить.
Переместимся на нижнюю строку, посмотрим на 4 клетку. В ней может быть либо 4, либо 1. Единица выбывает, т.к. в верхней строчке над этой клеткой тоже 1, значит там 4, а в клетке слева 1. Вернёмся к предпоследней строчке. Т.к. в 4 клетке 4, то в этой строчке там будет 2. Четыре же будет над единицей.
Дальше действуем аналогично и получаем результат на рисунке:
1. Преобразуйте уравнение (х + 7)2 - 4х = 2х(х - 5) к виду ax2 + bx + c = 0. Укажите старший коэффициент, второй коэффициент и свободный член этого уравнения.
Переобразуем:
Переносим в общую сторону (левую) и меняем знаки:
Сокрашаем:
ответ:
Старший коэффициент:
Второй коэффициент: 8x
Свободный член: -14
2. а) Определите, какое из уравнений является неприведенным квадратным уравнением и найдите его корни:
А)
В)
С)
D)
У неприведенных квадратных уравнениях, старшие коэффициенты не равны 1. (0/5, 3, 5, -17, тд - все неприведенные квадратные уравнения).
Решаем, как в Судоку.
Посмотрим на клетку, находящуюся в левом верхнем углу, по условию задачи, в этой клетке не 5,4,3, но это не 1 т.к. оно больше какого-то числа. Следовательно там 2. Тогда в клетке, что ниже 1.
Посмотрим на самую нижнюю клетку этого столбца - она может быть или 3 или 5. Посмотрим всю строчку. В строке есть 3, значит в этой клетке 5.
В итоге первый столбец : 2 1 4 3 5, а верхняя строка 2 3 5 1 4.
Теперь заполним 2 столбец.
В нём два знака > и туда подойдут 4 и 5(не 3 т.к. она наверху) Рядом с 4 не может быть 4, поэтому ставим 5, а две клетки ниже 4. Остаётся 2 и 1. Посмотрим на соседний столбец и в итоге получаем : 3 4 5 1 2(4 и 2 не работает)
Заполним предпоследнюю строку(там есть знак). В и клеточке, слева от которой стоит знак будет 5, так как 2 больше только 1, а 1 стоит выше, а 3 и 4 в этом столбике есть. Оставим пока так и перейдем к тем строчкам, которые мы можем теперь заполнить.
Переместимся на нижнюю строку, посмотрим на 4 клетку. В ней может быть либо 4, либо 1. Единица выбывает, т.к. в верхней строчке над этой клеткой тоже 1, значит там 4, а в клетке слева 1. Вернёмся к предпоследней строчке. Т.к. в 4 клетке 4, то в этой строчке там будет 2. Четыре же будет над единицей.
Дальше действуем аналогично и получаем результат на рисунке:
1. Преобразуйте уравнение (х + 7)2 - 4х = 2х(х - 5) к виду ax2 + bx + c = 0. Укажите старший коэффициент, второй коэффициент и свободный член этого уравнения.
Переобразуем:
Переносим в общую сторону (левую) и меняем знаки:
Сокрашаем:
ответ: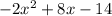
Старший коэффициент: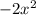
Второй коэффициент: 8x
Свободный член: -14
2. а) Определите, какое из уравнений является неприведенным квадратным уравнением и найдите его корни:
А)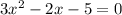
В)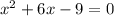
С)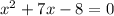
D)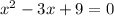
У неприведенных квадратных уравнениях, старшие коэффициенты не равны 1. (0/5, 3, 5, -17, тд - все неприведенные квадратные уравнения).
A)
2. б) Составьте приведенное квадратное уравнение, имеющие корни х1= 8, х2 = –2.
По теореме Виета:
ответ: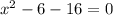
3. Дано квадратное уравнение 2х^2 - 16х + с = 0.
а) Определите, при каких значениях параметра с уравнение имеет два одинаковых корня.
Если дискриминант (D) квадратного уравнения равен 0, то уравнение имеет 1 корень, или говорят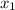
и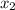 
совпадают.
Если p = 0, то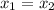
ответ: c = 32
3. б) Найдите эти корни уравнения
ответ: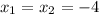
Дальше не знаю как решать