(1/4)^x-1 >=x+6

Найти целое решение нер-ва

:

(С ФСУ)

Выражение делится на число тогда, когда один из множителей делится на число

41 + 19 = 60, 60 делится на 60, следовательно и сумма будет делится

:

(Более замороченный)

Для этого можно просто доказать кратность этого выражения на множители числа 60.

60 =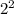 * 3 * 5

41, при делении на 5, дает остаток 1 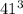 ( так же будет давать этот остаток)

19, при делении на 5, дает остаток 4 (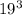 так же будет давать этот остаток)

1 + 4 = 5 : 5

Сумма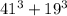 будет делится на 4 ( по признаку деления на 4, сумма будет оканчиваться на 0)

А деление на 3 можно доказать суммой цифр, 4+1 = 5 (остаток, при делении на 3, 2), 1 + 9 = 10 (остаток, при делении на 3, 1)

1 + 2 = 3 : 3

чтд

1) на формулы сокращенного умножения
2) на формулы сокращенного умножения и вынесение общего множителя
3) на формулы сокращенного умножения
4) решение квадратных уравнений и вынесение общего множжителя
5) Чтобы доказать делимость, разделим данное выражение на 8. Раскроем скобки, вынесем общий множитель и получим квадратное выражение.

Натуральные числа - это числа больше нуля, следовательно и полученное нами квадратное выражение должно быть больше нуля. Получаем квадратное неравенство, которое и решаем.

Т.к. при  коэффициент положительный, ветви параболы смотрят вверх, следовательно больше нуля заштрихованная область.

Нам же нужны значения n>0, а они входят в ответ. Значит данное в условии выражение делится на 8 при любом натуральном n. Что и требовалось доказать.