1. [ ] (4x-5) Приведите уравнение (2x + 1) -3x (3-2x) к форме ax2 + bx + c = 0 и укажите первый, второй, пустой член. 2.a) [ ] Построить квадратное уравнение для заданных корней:
А) х + 3х2 - 7 = 0
Б) - х2 + 5х - 2 = 0
В) 4x2 - 8x + 12 = 0
E) 9x + x2 - 2 = 0
б) [ ] Построить квадратное уравнение для заданных корней:
х1 = -7, х2 = 2.
А) х2 + 5х -14 = 0
Б) - х2 + 2х - 7 = 0
Б) х2 - 3х - 10 = 0
D) - x2 - 3x + 10 = 0
Д) х2 - 3х +7 = 0
[ ] Дано квадратное уравнение 3x2 - 6x + c = 0.
а) При каком значении параметра c существуют два взаимно равных корня уравнения. б) Найдите эти корни уравнения
[ ] Найдите следующее, не находя корней уравнения 2x2 - 5x -4 = 0:
а) х1 х24 + х2 х14
б) 1 / (x_1 ^ 2) + 1 / (x_2 ^ 2)
5. [ ] для треугольника x2–6x + 5 квадратов:
а) вычесть весь квадрат;
б) Разделите квадратичную троицу на множители
[ ] Решите уравнение: х2 - 8 | х | + 12 = 0
Группа точек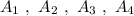 имеют одинаковую абсциссу х=4 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид
имеют одинаковую абсциссу х=4 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 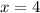 .
.
Группа точек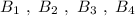 имеют одинаковую абсциссу х=2 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид
имеют одинаковую абсциссу х=2 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 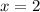 .
.
Группа точек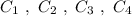 имеют одинаковую абсциссу х= -2 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид
имеют одинаковую абсциссу х= -2 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид  .
.
Группа точек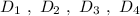 имеют одинаковую абсциссу х= -4 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид
имеют одинаковую абсциссу х= -4 , но различные ординаты. Эти точки лежат на прямой, параллельной оси ординат, уравнение этой прямой имеет вид 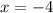 .
.
Точки, имеющие одинаковую абсциссу, на координатной плоскости лежат на одной прямой, параллельной оси ОУ.
Уравнение такой прямой имеет вид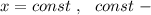 это число (константа- постоянная величина ) .
это число (константа- постоянная величина ) .
Благоприятных случаев: ?
1*1 = 1 (<10)
1*2 = 2 (<10)
1*3 = 3 (<10)
1*4 = 4 (<10)
1*5 = 5 (<10)
1*6 = 6 (<10)
2*1 = 2 (<10)
2*2 = 4 (<10)
2*3 = 6 (<10)
2*4 = 8 (<10)
2*5 = 10 (=10)
2*6 = 12 (>10)
3*1 = 3 (<10)
3*2 = 6 (<10)
3*3 = 9 (<10)
3*4 = 12 (>10)
3*5 = 15 (>10)
3*6 = 18 (>10)
4*1 = 4 (<10)
4*2 = 8 (<10)
4*3 = 12 (>10)
4*4 = 16 (>10)
4*5 = 20 (>10)
4*6 = 24 (>10)
5*1 = 5 (<10)
5*2 = 10 (=10)
5*3 = 15 (>10)
5*4 = 20 (>10)
5*5 = 25 (>10)
5*6 = 30 (>10)
6*1 = 6 (<10)
6*2 = 12 (>10)
6*3 = 18 (>10)
6*4 = 24 (>10)
6*5 = 30 (>10)
6*6 = 36 (>10)
Благоприятных случаев: 1 + 3 + 4 + 4 + 5 = 17
P =
Удачи!