1. Библиотекарь получила школьные учебники и решила размес- тить их по стеллажам. Она посчитала, что если поставить по 20
учебников на каждую полку, то две полки окажутся пустыми.
Но если на каждую полку поставить по 15 учебников, то на всех
полках будет одинаковое число книг. Сколько учебников полу-
чено библиотекой?
Можете полностью расписать

Показать ответ

Ответ:

voenngti

02.04.2022 08:41

Букв у нас 10, 3 буквы А, по 2 буквы М и Т, и по одной Е, И и К.
На первую позицию можно ставить одну из десяти букв, на вторую, одну из девяти и т.д. Получим: 10!
Найдём количество которыми можно составить слово математика из данного набора букв при учёте позиции той или иной буквы.
Е, И и К могут занимать только одну позицию, а вот А, М и Т можно менять местами.
Для М и Т это будет 2! и 2!, для А – 3!
С учётом порядка позиции их будет: 1*1*1*2!*2!*3! = 24

Тогда вероятность (согласно классическому определению): $\frac{24}{10!} = \frac{1}{151200}$

Попробуем другой, более простой
Перестановки с повторением.
Всего у нас $\frac{(1 + 1 + 1 + 2 + 2 + 3)!}{3!*2!*2!} = \frac{10!}{3!*2!*2!}$
Перестановка с повторением, которая даёт нам слово "Математика" всего одна, потому мы получаем вероятность:
$\frac{1}{\frac{10!}{3!*2!*2!}} = \frac{3!*2!*2!}{10!} = \frac{24}{10!} = \frac{1}{151200}$

0,0(0 оценок)

Ответ:

Mashaskliiiz

01.04.2022 11:43

1. -1,4

2. Одночленом не является то выражение, части которого не разделяются плюсом или минусом (К примеру, 2abc будет одночленом, а ab + 2c не будет, в общем, ab + 2c будет многочленом), в данном случае ответом будет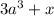 $3a^{3} + x$

3. Подобные слагаемые - те, которые имеют одну и ту же буквенную часть (Если одна буква возведена в одну степень, а другая в другую, они не будут подобными слагаемыми), при выполнении действий с ними, коэффициенты (Числа перед буквами) слагаются/вычисляются, в данном случае ответом будет 3a + 4b

4. При умножении одинаковых переменных степени слагаются, т.е., в данном случае будет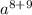 $a^{8 + 9}$ = $a^{17}$

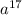
5.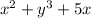 $x^{2} + y^{3} + 5x$ , как решать, я уже объяснял

6. 4y + 5 (8y - (4y - 5) = 8y - 4y + 5, так как перед скобкой стоит минус, остальное я уже объяснял)

7. 16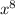 $x^{8}$ , так как, если после скобок стоит степень, степени внутри скобок умножаются на степень после скобок

8. 12x - 14 (Просто число перед скобками умножается на числа внутри скобок)

9.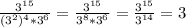 $\frac{3^{15}}{(3^{2})^4 * 3^6 } = \frac{3^{15}}{3^8 * 3^6 } = \frac{3^{15}}{3^{14}} = 3$ (В конце степени просто сокращаются, и остается только 3)

10.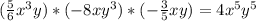 $(\frac{5}{6}x^3y) * (-8xy^{3}) * (-\frac{3}{5}xy) = 4x^{5}y^5$ (Коэффициенты сокращаются, и в итоге остается 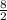$\frac{8}{2}$ , что равно 4, а результат положительный, так как отрицательное число, умноженное на отрицательное, становится положительным)