1)через какую точку по оси у проходит график функции заданный формулой у=5х+4 2) через какую точку по оси х проходит график функции заданный формулой у=-4х+8
Двухзачные числа- т.е. от 10 до 99. Всего это 99-10+1=90 чисел
т.к. мы выбираем случайно одно из этих чисел, то вероятность того, что оно окажется кратным зависит от количества кратных среди них.
Например, если из ста чисел кратных будет сто, то вероятность выпадения кратного числа равна 100/100 = 1 (если написать в процентах, то это 100%)
а если только одно, из ста то 1/100 = 0,01 (т.е. это 1%)
Чтобы посчитать количество кратных чисел в диапазоне от 10 до 99, можно поступить так: найти первое кратное число в диапазоне, и первое кратное, идущее после диапазона. Затем их разность делим на то число, количество кратных которому мы ищем.
Для четырёх: первое кратное в диапазоне- это 12, а первое кратное после диапазона- это 100
Для пяти, соответственно будет: 10, 100, и (100 - 10) / 5 = 90 / 5 = 18 (чисел, кратных пяти)
Далее: чтобы число было кратным четырём и пяти одновременно, нужно чтобы оно делилось на 4*5, т.е. на двадцать (здесь наименьшее общее кратное находится просто перемножением, так как 4 и 5 -это взаимно простые числа).
Соответственно, для 20-ти будет: 20, 100, и (100 - 20) / 20 = 80 / 20 = 4 (четыре числа, кратных четырём и пяти одновременно)
Без взятия производных для определения наибольшего и наименьшего значений функции приходится строить график этой функции.
График функции можно получить из графика следующим образом:
1. График сдвигаем по оси аргументов на 2 единицы вправо (так как -2). Либо ось аргументов сдвигаем влево. Смотри рисунок.
2. Полученный график y сдвигаем по оси значений функции на 4 единицы вверх (так как +4). Либо ось значений сдвигаем относительно графика вниз.
Полученный график функции показан самым жирным и самым синим на рисунке.
Из графика видим, что на отрезке рассматриваемая функция монотонно возрастает и наименьшим значением будет значение в точке начала отрезка, а наибольшим — в точке конца.
По-моему решить можно так:
Двухзачные числа- т.е. от 10 до 99. Всего это 99-10+1=90 чисел
т.к. мы выбираем случайно одно из этих чисел, то вероятность того, что оно окажется кратным зависит от количества кратных среди них.
Например, если из ста чисел кратных будет сто, то вероятность выпадения кратного числа равна 100/100 = 1 (если написать в процентах, то это 100%)
а если только одно, из ста то 1/100 = 0,01 (т.е. это 1%)
Чтобы посчитать количество кратных чисел в диапазоне от 10 до 99, можно поступить так: найти первое кратное число в диапазоне, и первое кратное, идущее после диапазона. Затем их разность делим на то число, количество кратных которому мы ищем.
Для четырёх: первое кратное в диапазоне- это 12, а первое кратное после диапазона- это 100
посчитаем количество кратных четырём: (100 - 12) / 4 = 88 / 4 = 22 (т.е. в нашем диапазоне 22 числа, кратных четырём)
Для пяти, соответственно будет: 10, 100, и (100 - 10) / 5 = 90 / 5 = 18 (чисел, кратных пяти)
Далее: чтобы число было кратным четырём и пяти одновременно, нужно чтобы оно делилось на 4*5, т.е. на двадцать (здесь наименьшее общее кратное находится просто перемножением, так как 4 и 5 -это взаимно простые числа).
Соответственно, для 20-ти будет: 20, 100, и (100 - 20) / 20 = 80 / 20 = 4 (четыре числа, кратных четырём и пяти одновременно)
Далее, найдём вероятности выпадения кратных чисел:
кратных четырём: 22 / 90 = 0,2444 (округлил до 4 знаков после запятой)
кратных пяти: 18 / 90 = 0,2
кратных четырём и пяти: 4 / 90 = 0,0444 (тоже округл. до 4 знаков)
Без взятия производных для определения наибольшего и наименьшего значений функции приходится строить график этой функции.
График функции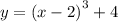 можно получить из графика
можно получить из графика 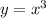 следующим образом:
следующим образом:
1. График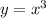 сдвигаем по оси аргументов на 2 единицы вправо (так как -2). Либо ось аргументов сдвигаем влево. Смотри рисунок.
сдвигаем по оси аргументов на 2 единицы вправо (так как -2). Либо ось аргументов сдвигаем влево. Смотри рисунок.
2. Полученный график y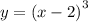 сдвигаем по оси значений функции на 4 единицы вверх (так как +4). Либо ось значений сдвигаем относительно графика вниз.
сдвигаем по оси значений функции на 4 единицы вверх (так как +4). Либо ось значений сдвигаем относительно графика вниз.
Полученный график функции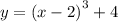 показан самым жирным и самым синим на рисунке.
показан самым жирным и самым синим на рисунке.
Из графика видим, что на отрезке![\left[0;3\right]](/tpl/images/0129/5065/c1b3c.png) рассматриваемая функция монотонно возрастает и наименьшим значением будет значение в точке начала отрезка, а наибольшим — в точке конца.
рассматриваемая функция монотонно возрастает и наименьшим значением будет значение в точке начала отрезка, а наибольшим — в точке конца.
Итак, ответ.