Объяснение:
1)
D(f) =R
Внутренние точки области определения, в которых производная равна нулю или не существует, называются критическими точками.
ответ : -1; 2.
2)
D(f) =[0; +∞)
- критическая точка .
При переходе через эту точку производная меняет свой знак с "+"
на "-". Значит - точка максимума .
Найдем значение функции в данной точке . Это и будет максимум функции
ответ : - максимум функции.
Объяснение:
1)
D(f) =R
Внутренние точки области определения, в которых производная равна нулю или не существует, называются критическими точками.
ответ : -1; 2.
2)
D(f) =[0; +∞)
При переходе через эту точку производная меняет свой знак с "+"
на "-". Значит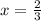 - точка максимума .
- точка максимума .
Найдем значение функции в данной точке . Это и будет максимум функции
ответ :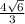 - максимум функции.
- максимум функции.