1.Из пункта О в одном направлении, но в разное время (t₁ = 0 и t₂ = 2 ч) с одинаковой скоростью(v₁ = v₂ = 4 км/ч) вышли два человека. Поставь в соответствие двум процессам линейные функции и построй графики. Произойдёт ли их встреча, если условия движения не изменятся?
2. Из пункта О в разное время (t₁ = 0 и t₂ = 1 ч) с разной скоростью (v₁ = 2км/ч и v₂ = 4 км/ч) в одном направлении вышли два пешехода. Поставь в соответствие двум процессам линейные функции и построй графики. Используя график движения, ответь на во на каком расстоянии от пункта О они встретятся?
3. Из пунктов О и А, расстояние между которыми 2 км, одновременно (t = 0) с одинаковой скоростью v₁ = v₂ = 5 км/ч в одном направлении выехали две гружёные повозки. Поставь в соответствие двум процессам линейные функции и постройте графики. Используя график движения, ответь на во какое расстояние будет между ними через 2 ч после начала движения УМОЛЯЮ
Сначала просто решим неравенство методом интервалов:
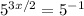 ;
;
Найдём корни числителя:
3x/2=-1;
x= -2/3;
Найдём корни знаменателя:
x-4=0;
x=4;
Теперь начертим числовую прямую, отметим на ней точки -2/3 и 4 и посмотрим, где всё выражение принимает значения больше нуля (числовая прямая прикреплена).
Мы видим, что всё выражение больше нуля при x>4 и x< -2/3
Поскольку нам нужен наименьшее целое положительное решение, мы берём число 5 (4 мы взять не можем, т.к. в знаменателе будет 0 и потому, что 4 не входит в получившиеся лучи).
ответ: 5.
Скорее всего здесь речь идет об убывающей геометрической прогрессии...
для убывающей геометрической прогрессии Sn -> b1 / (1-q)
b1 / (1-q) = 3/4 ___ 4b1 = 3(1-q)
и сумма кубов тоже будет убывающей... => Sn3 -> (b1)^3 / (1-q^3)
(b1)^3 / (1-q^3) = 27/208
27(1-q)^3 / (64(1-q^3)) = 27/208
(1-q)^3 / ((1-q)(1+q+q^2)) = 4/13
(1-q)^2 / (1+q+q^2) = 4/13
13(1-2q+q^2) = 4(1+q+q^2)
13-26q+13q^2 - 4-4q-4q^2 = 0
3q^2 - 10q + 3 = 0
D = 100 - 4*9 = 64
q1 = (10 + 8)/6 = 3 ___ q2 = (10 - 8)/6 = 1/3
b1 = 1/2
Сумма квадратов членов прогрессии = (b1)^2 / (1-q^2) = 1/4 : 8/9 = 1/4 * 9/8 = 9/32