1. Постройте график функции y = −2x + 1. Найдите:

а) Значение функции, если значение аргумента равно: 3; -2,5; 0;

б) Значение аргумента, при котором значение функции равно: 5; -2; 0.

2. Постройте график функции: =13(−3)2+3.

Укажите:

а) Область определения функции;

б) Область значений функции;

в) Координату вершины параболы;

г) Укажите наибольшее (или наименьшее) значение функции;

д) Укажите промежутки возрастания и убывания функции;

е) Запишите уравнение оси параболы.

3. Постройте график функции: =5+2+3.

Укажите:

а) Область определения функции;

б) Область значений функции;

в) Укажите наибольшее (или наименьшее) значение функции;

г) Укажите промежутки возрастания и убывания функции;

д) В каких координатных четвертях расположен график данной функции?

4. Постройте график функции = 2−6+5.

Укажите:

а) Область определения функции;

б) Область значений функции;

в) Координату вершины параболы;

г) Укажите наибольшее (или наименьшее) значение функции;

д) Укажите промежутки возрастания и убывания функции;

е) Определите, при каких значениях аргумента функция принимает положительные; отрицательные значения.

Показать ответ

Ответ:

taniataolia

17.05.2022 06:27

1. Сумма углов n-угольника равна 180°(n-2).

В случае 12-угольника сумма равна 1800 градусов. Т. к. он правильный, то углы его равны 1800/12=150 градусов. ответ : 150°

2. Площадь параллелограмма равна произведению его основания (a) на высоту (h):

S = a ⋅ h

144 см² = а ⋅ 16 см

a = 9 см

3.s = a * b / 2

a - катет b - катет

a = 12

b^2 = 13^2 - 12^2

b^2 = 169 - 144

b^2 = 25

b = 5

S = 5 * 12 / 2

S = 30

4. Площадь ромба можно найти по формуле S = 0,5d₁d₂, где d₁ и d₂ - его диагонали.

Т.к. ромб - это параллелограмм, у которого все стороны равны, то он обладает всеми свойствами параллелограмма, а именно: диагонали ромба точкой пересечения делятся пополам. Значит, полусумма диагоналей равна 28 : 2 = 14 (см).

Свойство ромба: диагонали ромба перпендикулярны. Значит, при пересечении диагоналей ромба получаются 4 прямоугольных треугольника, у которых катеты - половины диагоналей, а гипотенуза - сторона ромба.

Рассмотрим один из прямоугольных треугольников и, применив теорему Пифагора, найдем его катеты.

Пусть один из катетов х см, тогда второй будет равен (14 - х) см. Т.к. сторона ромба равна 10 см, то составим и решим уравнение:

х² + (14 - х)² = 10²,

х² + 196 - 28х + х² - 100 = 0,

2х² - 28х + 96 = 0,

х² - 14х + 48 = 0.

D = (-14)² - 4 · 1 · 48 = 196 - 192 = 4; √4 = 2

х₁ = (14 + 2)/(2 · 1) = 16/2 = 8, х₂ = (14 - 2)/(2 · 1) = 12/2 = 6

Если один из катетов равен 8 см, то второй будет равен 14 - 8 = 6 (см). Тогда диагонали ромба будут равны 16 см и 12 см, а площадь

S = 0,5 · 16 · 12 = 96 (см²)

Если один из катетов равен 6 см, то второй будет равен 14 - 6 = 8 (см). Тогда диагонали ромба будут равны 12 см и 16 см, а площадь

S = 0,5 · 12 · 16 = 96 (см²)

ответ: 96 см².

5.Обозначим трапецию АВСД. угол С=угол Д=90 градусов. так как в трапецию можно вписать окружность, то суммы противоположных сторон равны ВС+АД=СД+АВ.

проведём высоту ВК. Она разделила трапецию на прямоугольник ДСВК и прямоугольный треугольник АВК. Так как острый уголА = 45 градусов, то второй острый угол АВК = 90-45=45 градусов, значит треугольник равнобедренный, ВК=АК.

Пусть АК=х тогда и ВК=х, по т. Пифагора х²+х²=(12√2)², 2х²=144·2, х²=144, х=12, АК=12 см, ВК=12 см, тогда и СД=12 см.S(ABCD)=1/2·(АД+ВС)·ВК=1/2·(12+12√2)·12=72·(1+√2)

0,0(0 оценок)

Ответ:

дангалах

17.05.2022 00:25

1. 2)

2. 3)

Объяснение:

1.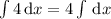 $\int {4}\, \text{d}x = 4 \int\, \text{d}x$ , интеграл 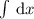$\int \, \text{d}x$ табличный и равняется 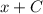x + C , тогда исходный равняется 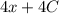4x + 4C , произведение констант — тоже константа, поэтому решением будет 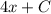4x+C , что соответствует второму варианту ответа.

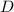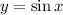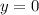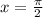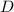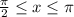2. Область , ограниченная указанными кривыми $y=\sin x$ , y=0 , $x= \pi$ и $x=\frac{\pi}{2}$ , показана на приложенном рисунке. Получается, что задают два неравенства, $0 \leq y \leq \sin x$ и $\frac{\pi}{2} \leq x \leq \pi$ . Первое неравенство задаёт подынтегральную функцию, притом напрямую (так как левая часть неравенства равна нулю), а второе — пределы интегрирования.

$\int\limits^\pi_\frac{\pi}{2} \sin{x} \, \text{d}x = (-\cos x)|^\pi_\frac{\pi}{2} = -\cos \pi - \left(-\cos \frac{\pi}{2}\right) = -(-1) - 0 = 1.$

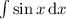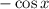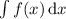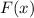(Так получается, ибо $\int \sin{x} \, \text{d}x$ — табличный интеграл, равный $-\cos x$ , а затем для определённого интегрирования применяется формула Ньютона-Лейбница, то есть $\int \limits_a^b {f(x)} \, \text{d}x = F(b) - F(a)$ , при известном $\int {f(x)} \, \text{d}x$ , то есть F(x) , притом константа в таком случае игнорируется.)