Відповідь:
1)2х(х-3) =0 2х=0, х1=0,х-3=0, х=3
Пояснення:
б)3(х²-25)=0 х=±5
х²-10х+25=0 х1+х2=10
х1*х2=25 х1=-5,х2=-5
4х²+6х+2=0 д=в²-4ас=6²-4*4*2=36-32=4 √4=2
х1=1,х2=3/2
3х²+8х+6=0 д=8²-4*3*6=64-72=-8 д∠0 корені не визначені
1.
a)
Делим уравнение на 2, тогда:
⇒
x = 0
Или:
х - 3 =
х = 3
б)
Переносим -75 вправо (с плюсом), тогда:
Делим на 3, откуда находим корень методом извлечения из результата деления на 3 квадратного корня, тогда:
2. Решаем квадратные уравнения через дискриминант:
а) Запишем исходное уравнение:
Находим дискриминант:
D =
,
А значит, данное уравнение имеет всего 1 корень!:
Відповідь:
1)2х(х-3) =0 2х=0, х1=0,х-3=0, х=3
Пояснення:
б)3(х²-25)=0 х=±5
х²-10х+25=0 х1+х2=10
х1*х2=25 х1=-5,х2=-5
4х²+6х+2=0 д=в²-4ас=6²-4*4*2=36-32=4 √4=2
х1=1,х2=3/2
3х²+8х+6=0 д=8²-4*3*6=64-72=-8 д∠0 корені не визначені
1.
a)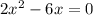
Делим уравнение на 2, тогда:
⇒
x = 0
Или:
х - 3 =
х = 3
б)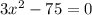
Переносим -75 вправо (с плюсом), тогда:
Делим на 3, откуда находим корень методом извлечения из результата деления на 3 квадратного корня, тогда:
2. Решаем квадратные уравнения через дискриминант:
а) Запишем исходное уравнение:
Находим дискриминант:
D =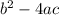
А значит, данное уравнение имеет всего 1 корень!: