По определению факторгруппы, "a" эквивалентно "b" тогда и только тогда, когда
Выберем какой-нибудь элемент группы . Подсчитаем, сколько элементов из группы эквивалентно этому элементу
Понятно, что таких элементов ровно 4 штуки:
--
--
--
--
Докажем, что например
Действительно, иначе было бы
Отсюда , что попросту неверно в
Аналогично рассматриваются другие случаи. Таким образом, любому элементу эквивалентно ровно 4 элемента группы G(включая сам элемент ). К тому же, в группе содержится 20 элементов
Объяснение:
По определению факторгруппы, "a" эквивалентно "b" тогда и только тогда, когда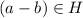
Выберем какой-нибудь элемент группы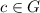
. Подсчитаем, сколько элементов из группы эквивалентно этому элементу
Понятно, что таких элементов ровно 4 штуки:
--
--
--
--
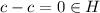
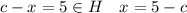
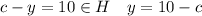
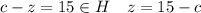
Докажем, что например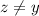
Действительно, иначе было бы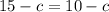
Отсюда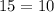
, что попросту неверно в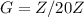 
Аналогично рассматриваются другие случаи. Таким образом, любому элементу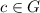
эквивалентно ровно 4 элемента группы G(включая сам элемент 
). К тому же, в группе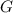 
содержится 20 элементов
Таким образом, в факторгруппе содержится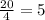
заметим
1. x! (x > 4) оканчивается на 0 (x! = 1*2*...*(x-1)*x есть 2 и 5 в умножении)
2. квадраты чисел могут оканчиваться на цифры 0, 1, 4, 5, 6, 9
1! + 2! + 3! + 4! = 1 + 1*2 + 1*2*3 + 1*2*3*4 = 1 + 2 + 6 + 24 = 33
после 4-х решений нет
33 - не квадрат, далее числа, которые оканчиваются на 3, что тоже не может быть квадратом
Смотрим x=1, 2 , 3
1. x = 1
1 = y²
y = 1
y = -1
2. x = 2
1! + 2! = y²
y² = 3 нет решений в целых числах
3. х = 3
1! + 2! + 3! = y²
y² = 1 + 2 + 6 = 9
y = 3
y = -3
ответ (1,1) (1,-1) (3,3) (3,-3)