1)составьте многочлен p(x)=p1(x)+p3(x)-4p2(x)
p1(x)=3x^2-2x
p2(x)=x+4
p3(x)=5x^2+7
p(x)=p3(x)-p2(x)+2p1(x)
2)преобразуйте заданное выражение в многочлен стандартного вида
3xy(2x^2-4y^3+x^2y^2)
(m+3)(m-7)
(24a^3b^2-8a^2b^3+16a^2b^2):8a^2b^2
3)у выражение используя формулы сокращённого умножения
(с НУЖНО ОЧЕНЬ
Объяснение:
4) x^2(3x + 1) - (x^2 + 1)^2 = 3
3x^3 + x^2 - x^4 - 2x^2 - 1 - 3 = 0
3x^3 - x^4 - x^2 - 4 = 0
x^4 - 3x^3 + x^2 + 4 = 0
Попробуем подобрать целые корни, они могут быть равны делителям свободного члена, т. е. 4
Проверим 1:
1 - 3 + 1 + 4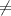 0 - не подходит
0 - не подходит
Проверим 2, 2 подходит, значит, можно выделить множитель x - 2
x^4 - 2x^3 - x^3 + 2x^2 - x^2 + 4 = 0
(x - 2)x^3 - x^2(x-2) -(x-2)(x+2) = 0
(x^3 - x^2 - x - 2)(x-2) = 0
x^3 - x^2 - x - 2 = 0
Здесь также подходит корень x = 2, выделим множитель x - 2
x^3 - 2x^2 + x^2 - 2x + x - 2 = 0
x^2(x-2) + x(x - 2) +(x - 2) = 0
(x^2 + x + 1)(x - 2) = 0
x^2 + x + 1 = 0
D = 1 - 4*1*1 = -3 - нет действительных корней
Получается, действительный корень только x = 2
2) (2x^2 - 1)^2 + x(2x - 1)^2 = (x + 1)^2 + 16x^2 - 6
4x^4 - 4x^2 + 1 + 4x^3 - 4x^2 + x = x^2 + 2x + 1 + 16x^2 - 6
4x^4 + 4x^3 - 25x^2 - x + 6 = 0
Подбираем корни - делители 6
x = 1 и x = -1 не подходит
x = 2 - подходит
4*16 + 4*8 - 100 - 2 + 6 = 96 - 100 - 2 + 6 = 0
Множитель x - 2
4x^4 - 8x^3 + 12x^3 - 24x^2 - x^2 + 2x - 3x + 6 = 0
(x - 2)(4x^3 + 12x^2 - x - 3) = 0
4x^3 + 12x^2 - x - 3 = 0
Подбираем корни - делители 3
x = -3 подходит
4 * (-27) + 12*9 + 3 - 3 = -108 + 108 = 0
Множитель x - (-3) = x + 3
4x^2(x + 3) - (x + 3) = 0
(2x - 1)(2x + 1)(x + 3) = 0
2x - 1 = 0 ⇒ x = 0.5
2x + 1 = 0 ⇒ x = -0.5
Итого 4 действительных корня x = 0.5, x = -0.5, x = -3, x = 2
Объяснение:
4) x^2(3x + 1) - (x^2 + 1)^2 = 3
3x^3 + x^2 - x^4 - 2x^2 - 1 - 3 = 0
3x^3 - x^4 - x^2 - 4 = 0
x^4 - 3x^3 + x^2 + 4 = 0
Попробуем подобрать целые корни, они могут быть равны делителям свободного члена, т. е. 4
Проверим 1:
1 - 3 + 1 + 4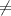 0 - не подходит
0 - не подходит
Проверим 2, 2 подходит, значит, можно выделить множитель x - 2
x^4 - 2x^3 - x^3 + 2x^2 - x^2 + 4 = 0
(x - 2)x^3 - x^2(x-2) -(x-2)(x+2) = 0
(x^3 - x^2 - x - 2)(x-2) = 0
x^3 - x^2 - x - 2 = 0
Здесь также подходит корень x = 2, выделим множитель x - 2
x^3 - 2x^2 + x^2 - 2x + x - 2 = 0
x^2(x-2) + x(x - 2) +(x - 2) = 0
(x^2 + x + 1)(x - 2) = 0
x^2 + x + 1 = 0
D = 1 - 4*1*1 = -3 - нет действительных корней
Получается, действительный корень только x = 2
2) (2x^2 - 1)^2 + x(2x - 1)^2 = (x + 1)^2 + 16x^2 - 6
4x^4 - 4x^2 + 1 + 4x^3 - 4x^2 + x = x^2 + 2x + 1 + 16x^2 - 6
4x^4 + 4x^3 - 25x^2 - x + 6 = 0
Подбираем корни - делители 6
x = 1 и x = -1 не подходит
x = 2 - подходит
4*16 + 4*8 - 100 - 2 + 6 = 96 - 100 - 2 + 6 = 0
Множитель x - 2
4x^4 - 8x^3 + 12x^3 - 24x^2 - x^2 + 2x - 3x + 6 = 0
(x - 2)(4x^3 + 12x^2 - x - 3) = 0
4x^3 + 12x^2 - x - 3 = 0
Подбираем корни - делители 3
x = -3 подходит
4 * (-27) + 12*9 + 3 - 3 = -108 + 108 = 0
Множитель x - (-3) = x + 3
4x^2(x + 3) - (x + 3) = 0
(2x - 1)(2x + 1)(x + 3) = 0
2x - 1 = 0 ⇒ x = 0.5
2x + 1 = 0 ⇒ x = -0.5
Итого 4 действительных корня x = 0.5, x = -0.5, x = -3, x = 2