1). В арифметической прогрессии а1 = 30, d = -11. Найти a4 и а21.
2). В арифметической прогрессии а1 = -5,а7 = 13. Найти d .
3). Найти разность и четвертый член арифметической прогрессии, если а1 = 43, а6 = 23.
4). Найти второй член арифметической прогрессии, если двадцать первый член этой прогрессии равен 52, а тридцать первый член равен 72.
5). Найти первый положительный член в арифметической прогрессии -12; -10…
6). В арифметической прогрессии первый ее член равен 10 , десятый член прогрессии равен 28. Найти сумму десяти первых членов прогрессии.
7). В арифметической прогрессии десятый член равен 13, пятый член равен 18. Найти разность прогрессии
1)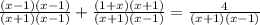
Область определения: x ≠ -1; x ≠ 1
(x - 1)^2 + (x + 1)^2 = 4
x^2 - 2x + 1 + x^2 + 2x + 1 - 4 = 0
2x^2 - 2 = 0
2(x^2 - 1) = 0
2(x + 1)(x - 1) = 0
x1 = -1; x2 = 1
Оба корня не подходят по области определения.
Решений нет.
2)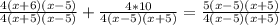
Область определения: x ≠ -5; x ≠ 5
4(x^2 + x - 30) + 40 = 5(x^2 - 25)
4x^2 + 4x - 120 + 40 = 5x^2 - 125
0 = x^2 - 4x - 45
(x - 9)(x + 5) = 0
x = -5 не подходит по области определения
x = 9 подходит.
3)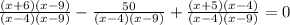
Область определения x ≠ 4; x ≠ 9
x^2 - 3x - 54 - 50 + x^2 + x - 20 = 0
2x^2 - 2x - 124 = 0
x^2 - x - 62 = 0
D = 1 - 4(-62) = 249
x1 = (1 - √249)/2; x2 = (1 + √249)/2
Но я предполагаю, что в задаче опечатка, должно быть:
Тогда получается уравнение
x^2 - x - 12 = 0
(x - 4)(x + 3) = 0
Подходит только корень
x = -3
1 раствор 2 раствор 3раствор/3раствор смесь/смесь
14% 50% 0% / 50% 22% / 32%
х кг у кг 10кг / 10кг х+у+10 кг/ х+у+10 кг
теперь пользуясь данными таблицы составим уравнение
(смешивая растворы СКЛАДЫВАТЬ мы можем только массы!)
14% от х кг это 0,14х кг
50% от у кг это 0,5у кг
22% от (х+у+10) кг это 0,22(х+у+10) кг
32% от (х+у+10) кг это 0,32(х+у+10)кг
50% от 10 кг это 5 кг
теперь уравнение
Вычтем из второго уравнения первое
подставим в первое
Значит первого раствора было 25 кг, второго 15 кг